题目内容
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在
在![]() 轴的正半轴上),与
轴的正半轴上),与![]() 轴交于点
轴交于点![]() ,矩形
,矩形![]() 的一条边
的一条边![]() 在线段
在线段![]() 上,顶点
上,顶点![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() 上.
上.

![]() 求点
求点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
![]() 若点
若点![]() 的坐标为
的坐标为![]() ,矩形
,矩形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数表达式,并指出
的函数表达式,并指出![]() 的取值范围;
的取值范围;
![]() 当矩形
当矩形![]() 的面积
的面积![]() 取最大值时,
取最大值时,
①求直线![]() 的解析式;
的解析式;
②在射线![]() 上取一点
上取一点![]() ,使
,使![]() ,若点
,若点![]() 恰好落在该抛物线上,则
恰好落在该抛物线上,则![]() ________.
________.
【答案】⑴:![]() ,
,![]() ,
,![]() ;⑵
;⑵![]() ;⑶:①
;⑶:①![]() ;②
;②![]() .
.
【解析】
(1)令x=0求出抛物线与x轴的交点坐标,令x=0求出抛物线与y轴交点坐标;
(2)先表示出BE,DE,用矩形的面积公式求解即可;(3)①由(2)得到的矩形面积的函数关系式,面积最大时求出m,从而确定出D,F坐标,即可得出直线解析式;②先确定出直线DF和抛物线的交点坐标,用比例式求出k.
(1)∵抛物线![]() 与x轴交于A,B两点(点A在x轴的正半轴上),∴令y=0,即
与x轴交于A,B两点(点A在x轴的正半轴上),∴令y=0,即![]() ,∴x=-4或x=2,令
,∴x=-4或x=2,令![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]() ,
,![]() ;
;
(2)由(1)知,OA=2,OC=4,AD=2-m,∵DG∥OC,∴![]() ,∴DG=4-2m,同理BE=4-2m,∴DE=AB-AD-BE=3m,∴
,∴DG=4-2m,同理BE=4-2m,∴DE=AB-AD-BE=3m,∴![]() ;
;
(3)①由(2)得,![]() ;当m=1时,矩形DEFG面积最大,最大面积为6,此时,
;当m=1时,矩形DEFG面积最大,最大面积为6,此时,![]() ,
,![]() ,
,![]() ,
,![]() ,∴直线DF的解析式为
,∴直线DF的解析式为![]() ;
;
②如图
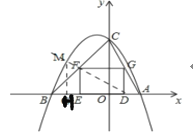
由①知,D(1,0),F(-2,2),∴![]() ,∴FM=k×DF=
,∴FM=k×DF=![]() ,过点M作MH⊥x轴,设
,过点M作MH⊥x轴,设![]() 则
则![]() ∴
∴![]() ,∵点M在抛物线上,∴
,∵点M在抛物线上,∴![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∵
,∵![]() ,
,![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,故答案为
,故答案为![]() .
.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目