Question

已知Rt△ABC中，∠C=90°，AC="3" ， BC=4，则△ABC的内切圆的半径是         ．

Answer 1

1

试题分析：Rt△ABC中，∠C=90°，AC="3" ， BC=4，由勾股定理得AB=5；△ABC的内切圆是圆O，如图所示，G、E、F分别是内切圆与Rt△ABC三边BC、AC、AB的切点，连接OG、OE、OF，设AF=x,根据三角形内切圆的性质那么AE=x;BF=5-x，因此BG=5-x,因为BC=4，所以CG=x-1，所以CE=x-1,因为AC=3，所以CE+AE=3，解得x=2，所以CE="2-1=1," Rt△ABC中，∠C=90,根据三角形内切圆的性质，OC是∠C的角平分线，OE⊥AC，所以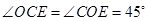，所以OE=CE=1，OE是三角形内切圆的半径，所以△ABC的内切圆的半径是1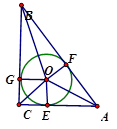

点评：本题考查内切圆，学生解答本题的关键是掌握三角形内切圆的性质，熟悉三角形内切圆的性质，熟悉勾股定理