Question

如图，△ACB和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°，D为AB边上的点，求证： (1)△ACE≌△BCD； (2)AD2＋DB2＝DE2．

Answer 1

答案：
解析：

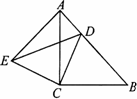
证明：(1)∵∠ACB＝∠ECD＝90°． 　　即∠ACD＋∠BCD＝∠ACD＋∠ACE， 　　∴∠BCD＝∠ACE． 　　∵△ACB和△ECD都是等腰直角三角形． 　　∴BC＝AC，DC＝EC， 　　∴△ACE≌△BCD． 　　(2)∵△ACB是等腰直角三角形， 　　∴∠B＝∠BAC＝45°． 　　由(1)知，△ACE≌△BCD，∴∠CAE＝∠B＝45°，AE＝BD． 　　∴∠DAE＝∠CAE＋∠BAC＝45°＋45°＝90°． 　　∴AD2＋AE2＝DE2． 　　即AD2＋DB2＝DE2．