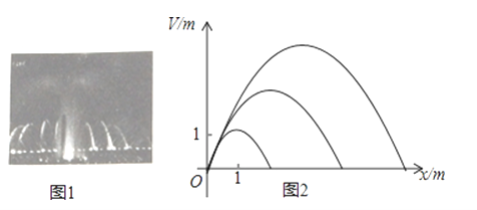
题目内容
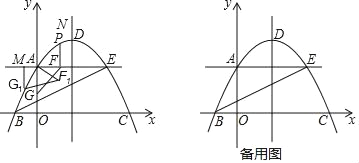
【题目】如图,射线OP与x轴正半轴的夹角为30°,点A是OP上一点,过点A作x轴的垂线与x轴交于点E.△AOE绕着点O逆时针旋转90°后能与△BOC重合,△BOC沿着y轴翻折能与△DOC重合,若点D恰好在抛物线y=x2(x>0)上,则点A的坐标是_____.
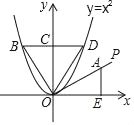
【答案】(3,![]() )
)
【解析】
设AE=t,利用含30度的直角三角形三边的关系别说出OE得到A(![]() t,t),再利用旋转的性质得到B(﹣t,
t,t),再利用旋转的性质得到B(﹣t,![]() t),接着利用关于y轴对称点的坐标特征得到D(t,
t),接着利用关于y轴对称点的坐标特征得到D(t,![]() t),然后把D(t,
t),然后把D(t,![]() t)代入y=x2得t2=
t)代入y=x2得t2=![]() t,最后解方程求出t即可得到点A的坐标.
t,最后解方程求出t即可得到点A的坐标.
设AE=t,
在Rt△AOE中,∵∠AOE=30°,
∴OE=![]() AE=
AE=![]() t,
t,
∴A(![]() t,t),
t,t),
∵△AOE绕着点O逆时针旋转90°后能与△BOC重合,
∴BC=AE=t,OC=OE=![]() t,
t,
∴B(﹣t,![]() t),
t),
∵△BOC沿着y轴翻折能与△DOC重合
∴D(t,![]() t),
t),
把D(t,![]() t)代入y=x2得t2=
t)代入y=x2得t2=![]() t,解得t1=0(舍去),t2=
t,解得t1=0(舍去),t2=![]() ,
,
∴点A的坐标为(3,![]() ).
).
故答案是:(3,![]() ).
).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目