Question

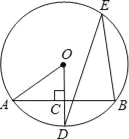
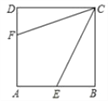
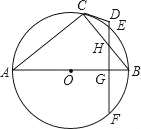
【题目】如图，已知AB是⊙O的直径，BC、EF是⊙O的弦，且EF垂直AB于点G，交BC于点H，CD与FE延长线交于D点，CD＝DH．

（1）求证：CD是⊙O的切线；

（2）若H为BC中点，AB＝10，EF＝8，求CD的长．

Answer 1

【答案】(1)见解析;(2).

【解析】

（1）要求证：DC是圆O的切线，只要证明OC⊥PC即可．

（2）先求出，CH=，FH=4+，进而判断出△DHM∽△BHG，即可得出结论．

（1）连接OD、OC相交于M，

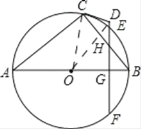
∵∠ACB＝90°，CO＝AO，

∴∠ACO＝∠CAO，∠CAO+∠B＝90°，∠B+∠BHG＝90°．

∴∠CAO＝∠BHG．

∵DC＝DH，

∴∠DCH＝∠DHC．

∴∠DCH＝∠ACO．

∴∠DCH+∠HCO＝∠ACO+∠OCH＝90°．

∴OC⊥PC．

即DC为切线．

（2）∵AB＝10，EF＝8，EF垂直AB，

∴EG＝4＝GF．

∴OG＝3，

∴BG＝2．

如图1，

在Rt△BFG中，BF＝

∵H为BC中点，

∴BH＝CH，

设EH＝x，则FH＝8﹣x，HG＝4﹣x，

根据相交弦定理得，BHCH＝EHFH，

∴BH2＝x（8﹣x），

在Rt△BHG中，BH2﹣HG2＝BG2，

∴x（8﹣x）﹣（4﹣x）2＝4，

∴x＝4+（舍）或x＝4﹣，

∴HG＝，BH＝CH＝，FH＝4+，

过点D作DM⊥CH于M，

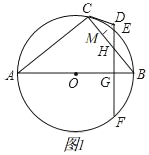
∵CD＝HD

∴MH＝CH＝

∵∠DHM＝∠BHG，∠DMH＝∠BGH＝90°，

∴△DHM∽△BHG，

∴，

∴，

∴DH＝，

∴CD＝．