Question

【题目】问题提出：如果一个多边形的各个顶点均在另一个多边形的边上，则称这个多边形为另一多边形的内接多边形

问题探究：

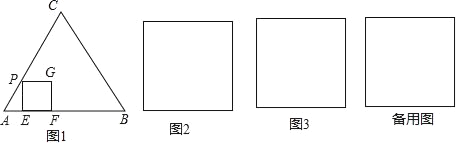
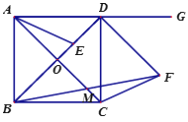
（1）如图1，正方形PEFG的顶点E、F在等边三角形ABC的边AB上，顶点P在AC边上．请在等边三角形ABC内部，以A为位似中心，作出正方形PEFG的位似正方形P'E'F'G'，且使正方形P'E'F'G'的面积最大（不写作法）

（2）如图2，在边长为4正方形ABCD中，画出一个面积最大的内接正三角形，并求此最大内接正三角形的面积

拓展应用：

（3）如图3，在边长为4的正方形ABCD中，能不能截下一个面积最大的直角三角形，并使其三边比为3：4：5，若能，请求出此直角三角形的最大面积，若不能，请说明理由．

Answer 1

【答案】（1）详见解析；（2）S△DEF＝16（2﹣3）；（3）能，S△DEF＝．

【解析】

（1）利用位似图形的性质，作出正方形PEFG的位似正方形P'E'F'G'，如图1所示；

（2）如图2，△DEF是最大内接正三角形，在AD上取一点M，使得EM=MD．由△DAE≌△DCF，推出∠ADE=∠CDF，由∠ADC=90°，推出∠ADE=∠CDF=15°，推出∠MED=∠MDE=15°，推出∠AME=∠MED+∠MDE=30°，设AE=a，则EM=DM=2a，AM=a，可得a+2a=4，推出a=4（2-），推出BE=BF=4（-1），由此即可解决问题．

（3）能．理由：如图3中，假设△BEF是直角三角形，EF：BE：BF=3：4：5，由△ABE∽△DEF，可得，AB=4，推出DE=3，AE=1，DF=，推出BE=，EF=，BF=，由此即可解决问题．

（1）如图1，正方形P'E'F'G'即为所求；

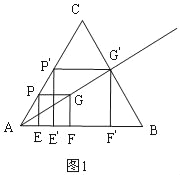
（2）如图2，△DEF是最大内接正三角形，在AD上取一点M，使得EM＝MD．

∵△DEF是等边三角形，

∴DE＝DF，∠EDF＝60°，

在Rt△DAE和Rt△DCF中，

，

∴△DAE≌△DCF，

∴∠ADE＝∠CDF，

∵∠ADC＝90°，

∴∠ADE＝∠CDF＝15°，

∴∠MED＝∠MDE＝15°，

∴∠AME＝∠MED+∠MDE＝30°，

设AE＝a，则EM＝DM＝2a，AM＝a，

∴a+2a＝4，

∴a＝4（2﹣），

∴BE＝BF＝4（﹣1），

∴S△DEF＝16﹣2××4×4（2﹣）﹣×4（﹣1）×4（﹣1）＝16（2﹣3）．

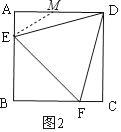
（3）能．理由：如图3中，假设△BEF是直角三角形，EF：BE：BF＝3：4：5，

∵∠A＝∠D＝∠BEF＝90°，

∴∠AEB+∠ABE＝90°，∠AEB+∠DEF＝90°，

∴∠ABE＝∠DEF，

∴△ABE∽△DEF，

∴，

∵AB＝4，

∴DE＝3，AE＝1，DF＝，

∴BE=，EF=，BF=，

∴△BEF满足条件，

∴S△DEF＝BEEF＝．