题目内容
【题目】求证：相似三角形面积的比等于相似比的平方．（请根据题意画出图形，写出已知，求证并证明）
【答案】证明见解析
【解析】
画出图形,写出已知,求证, 作AD⊥BC于D，A1D1⊥B1C1于D1然后根据相似三角形对应角可得∠B＝∠B1, ∠BDA＝∠B1D1A1，可得△ABD∽△A1B1D1， 
=k可得结论
已知：如图，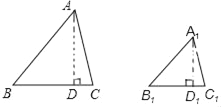
已知△ABC∽△A1B1C1，顶点A、B、C分别与A1、B1、C1对应，△ABC和△A1B1C1的相似比为k．
求证：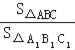
＝k2；
证明：作AD⊥BC于D，A1D1⊥B1C1于D1，
∵△ABC∽△A1B1C1，顶点A、B、C分别与A1、B1、C1对应，
∴∠B＝∠B1，
∵AD、A1D1分别是△ABC，△A1B1C1的高线，
∴∠BDA＝∠B1D1A1，
∴△ABD∽△A1B1D1，
∴=k
∴＝
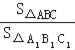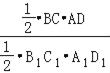＝k2．
练习册系列答案
相关题目
