题目内容
【题目】如图,顶点为D的抛物线y=﹣![]() x2+
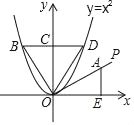
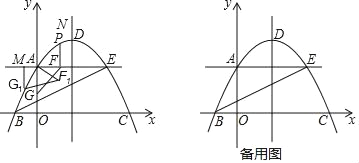
x2+![]() x+4与y轴交于点A,与x轴交于两点B、C(点B在点C的左边),点A与点E关于抛物线的对称轴对称,点B、E在直线y=kx+b(k,b为常数)上.
x+4与y轴交于点A,与x轴交于两点B、C(点B在点C的左边),点A与点E关于抛物线的对称轴对称,点B、E在直线y=kx+b(k,b为常数)上.
(1)求k,b的值;
(2)点P为直线AE上方抛物线上的任意一点,过点P作AE的垂线交AE于点F,点G为y轴上任意一点,当△PBE的面积最大时,求PF+FG+![]() OG的最小值;
OG的最小值;
(3)在(2)中,当PF+FG+![]() OG取得最小值时,将△AFG绕点A按顺时方向旋转30°后得到△AF1G1,过点G1作AE的垂线与AE交于点M.点D向上平移
OG取得最小值时,将△AFG绕点A按顺时方向旋转30°后得到△AF1G1,过点G1作AE的垂线与AE交于点M.点D向上平移![]() 个单位长度后能与点N重合,点Q为直线DN上任意一点,在平面直角坐标系中是否存在一点S,使以S、Q、M、N为顶点且MN为边的四边形为菱形?若存在,直接写出点S的坐标;若不存在,请说明理由.
个单位长度后能与点N重合,点Q为直线DN上任意一点,在平面直角坐标系中是否存在一点S,使以S、Q、M、N为顶点且MN为边的四边形为菱形?若存在,直接写出点S的坐标;若不存在,请说明理由.
【答案】(1)k=![]() ,b=1;(2)PF+FG+
,b=1;(2)PF+FG+![]() OG的最小值2+3
OG的最小值2+3![]() ;(3)存在,点S的坐标为:(﹣1,﹣1),(﹣1,9),(7,4).
;(3)存在,点S的坐标为:(﹣1,﹣1),(﹣1,9),(7,4).
【解析】
(1)由题意得:A(0,4)、B(-2,0)、D(3,![]() )、C(8,0)、E(6,4),则:过BE的直线为:y=
)、C(8,0)、E(6,4),则:过BE的直线为:y=![]() x+1;
x+1;
(2)设:P横坐标为m,则P(m,-![]() m2+
m2+![]() +4),H(m,
+4),H(m,![]() m+1),则:PH=-
m+1),则:PH=-![]() m2+
m2+![]() +4-(
+4-(![]() m+1)=-
m+1)=-![]() (x-2)2+4,当x=2时,PH取得最大值,此时△PEB的面积也取得最大值;构造与y轴夹角为45度的直线OR,如图所示,过点G作OR的垂线交OR于点R,则:RG=
(x-2)2+4,当x=2时,PH取得最大值,此时△PEB的面积也取得最大值;构造与y轴夹角为45度的直线OR,如图所示,过点G作OR的垂线交OR于点R,则:RG=![]() ,则:PF+FG+
,则:PF+FG+![]() OG=PF+FG+GR,当F、G、R三点共线时,FG+GR有最小值,即可求解;
OG=PF+FG+GR,当F、G、R三点共线时,FG+GR有最小值,即可求解;
(3)存在.当四边形为菱形,分在MNQ1S1的位置时、在MNQ2S2的位置时、在MNQ3S3的位置时三种情况分别求解.
(1)由题意得:A(0,4)、B(﹣2,0)、D(3,![]() )、C(8,0)、E(6,4),
)、C(8,0)、E(6,4),
则:过BE的直线为:y=![]() x+1;
x+1;
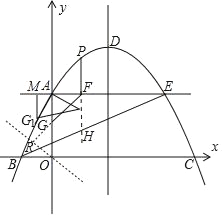
(2)延长PF交BE于点H,
设:P横坐标为m,则P(m,﹣![]() m2+
m2+![]() +4),H(m,
+4),H(m,![]() m+1),
m+1),
则:PH=﹣![]() m2+
m2+![]() +4﹣(
+4﹣(![]() m+1)=﹣
m+1)=﹣![]() (x﹣2)2+4,
(x﹣2)2+4,
当x=2时,PH取得最大值,此时△PEB的面积也取得最大值,
此时,P(2,6)、F(2,4),PF=2,
构造与y轴夹角为45度的直线OR,如图所示,过点G作OR的垂线交OR于点R,
则:RG=![]() ,∴PF+FG+
,∴PF+FG+![]() OG=PF+FG+GR,
OG=PF+FG+GR,
当F、G、R三点共线时,FG+GR有最小值,
在Rt△AGF中,AF=AG=2,则:GF=2![]() ,
,
在Rt△ROG中,RO=RG,OG=2,则:RG=![]() ,
,
FG+GR=2![]() +
+![]() =3
=3![]() ,
,
故:PF+FG+![]() OG的最小值2+3
OG的最小值2+3![]() ;
;
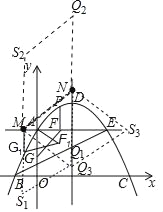
(3)存在.如图所示:
△AFG绕点A按顺时方向旋转30°后得到△AF1G1,
在Rt△G1AM中,AG1=2,∠AG1M=30°,
则:AM=1,∴M(﹣1,4),
点D向上平移![]() 个单位长度后能与点N重合,则:N(3,7),
个单位长度后能与点N重合,则:N(3,7),
则:MN=![]() =5,
=5,
当四边形为菱形,在MNQ1S1的位置时,MS1=MN=5,则点S1(﹣1,﹣1),
当四边形为菱形,在MNQ2S2的位置时,MS2=MN=5,则点S2(﹣1,9),
当四边形为菱形,在MNQ3S3的位置时,点S3与点M关于对称轴对称,则点S3(7,4),
故:所求点S的坐标为:(﹣1,﹣1),(﹣1,9),(7,4).

 阅读快车系列答案
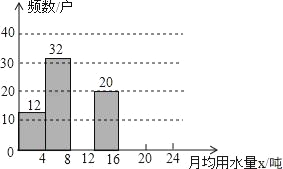
阅读快车系列答案【题目】2014年,河北省委宣传部主办“河北节约之星”活动,表彰节水先进典型,省委宣传部号召全社会以节水先进典型为榜样,牢固树立节约用水理念,争做节俭美德的传承者,节约用水的践行者.小鹏想了解某小区住户月均用水情况,随机调查了该小区部分住户,并将调查数据绘制成如图所示的频数分布直方图(不完整)和如下的频数分布表.
月均用水量x(吨) | 频数(户) | 频率 |
0<x≤4 | 12 | a |
4<x≤8 | 32 | 0.32 |
8<x≤12 | b | c |
12<x≤16 | 20 | 0.2 |
16<x≤20 | 8 | 0.08 |
20<x≤24 | 4 | 0.04 |
(1)求a,b,c的值,并将如图所示的频数分布直方图补充完整;
(2)求月均用水量超过12吨的住户占所调查总住户的百分比;
(3)若该小区有1000住户,根据所调查的数据,该小区月均用水量没有超过8吨的住户有多少?