题目内容
【题目】如图,在直角坐标系中,已知菱形ABCD的面积为15,顶点A在双曲线![]() 上,CD与y轴重合,且AB⊥x轴于B,AB=5.
上,CD与y轴重合,且AB⊥x轴于B,AB=5.
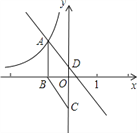
(1)求顶点A的坐标和k的值;
(2)求直线AD的解析式y1;
(3)在第二象限内,比较y与y1 的大小。
【答案】(1)顶点A的坐标为(-3,5),k的值为-15 ;(2)![]() ;
;
(3)当x<-3时,y<y1;当x=-3时,y=y1;当-3<x<0时,y>y1
【解析】(1)连接BD,作DE⊥AB,根据三角形的面积公式可得S菱形ABCD=2S△ABD,S△ABD=![]() AB×ED,再由菱形ABCD的面积为15,AB=5,可求得DE的长,即可求得A点的坐标,从而求得k的值;
AB×ED,再由菱形ABCD的面积为15,AB=5,可求得DE的长,即可求得A点的坐标,从而求得k的值;
(2)设点D的坐标为(0,y),则可得AB=AD=5,根据勾股定理可列方程求得点D的坐标,设直线AD的解析式为y=k′x+b,根据待定系数法列方程组求解即可.
(1)连接BD,作DE⊥AB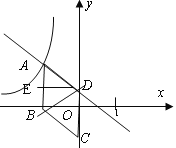
∴S菱形ABCD=2S△ABD,S△ABD=![]() AB×ED,
AB×ED,
∵菱形ABCD的面积为15,AB=5,
∴2×![]() ×5×ED=15,解得DE=3,
×5×ED=15,解得DE=3,
∴点A的坐标为(-3,5);
又∵点A在双曲线![]() 上,
上,
∴![]() ,解得k=-15;
,解得k=-15;
(2)设点D的坐标为(0,y)
∴AB=AD=5,
∴![]() ,解得y=9(舍去)或y=1,
,解得y=9(舍去)或y=1,
∴点D的坐标为(0,1).
设直线AD的解析式为y=k′x+b,
∵直线AD过A、D两点,
∴![]() ,解之得
,解之得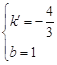
∴直线AD的解析式为![]() .
.
(3)当x<-3时,y<y1;当x=-3时,y=y1;当--3<x<0时,y>y1 .
“点睛”待定系数法求函数关系式是函数问题中极为重要的方法,再中考中比较常见,一般难度不大,需熟练掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目