题目内容
【题目】正方形OABC的边长为4,对角线相交于点P,抛物线L经过O,P,A三点,点E是正方形内的抛物线上的动点.
(1)建立适当的平面直角坐标系.
①直接写出O,P,A三点坐标;
②求抛物线L的表达式;
(2)求△OAE与△OCE面积之和的最大值.
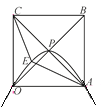
【答案】(1)建立平面直角坐标系见解析,①点O的坐标为(0,0),点A的坐标为(4,0),点P的坐标为(2,2);②抛物线L的表达式为y=-![]() x2+2x;(2)△OAE与△OCE面积之和最大值为9.
x2+2x;(2)△OAE与△OCE面积之和最大值为9.
【解析】试题分析:(1)以O点为原点,线段OA所在的直线为x轴,线段OC所在的直线为y轴建立直角坐标系.①根据正方形的边长结合正方形的性质即可得出点O、P、A三点的坐标;②设抛物线L的解析式为y=ax2+bx+c,结合点O、P、A的坐标利用待定系数法即可求出抛物线的解析式;(2)由点E为正方形内的抛物线上的动点,设出点E的坐标,结合三角形的面积公式找出S△OAE+SOCE关于m的函数解析式,根据二次函数的性质即可得出结论.
试题解析:(1)以O点为原点,线段OA所在的直线为x轴,线段OC所在的直线为y轴建立直角坐标系,如图所示.
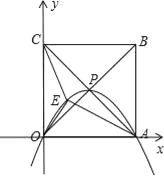
①∵正方形OABC的边长为4,对角线相交于点P,
∴点O的坐标为(0,0),点A的坐标为(4,0),点P的坐标为(2,2).
②设抛物线L的解析式为y=ax2+bx+c, ∵抛物线L经过O、P、A三点,
∴有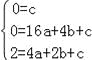 , 解得:
, 解得: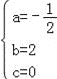 , ∴抛物线L的解析式为y=﹣
, ∴抛物线L的解析式为y=﹣![]() +2x.
+2x.
(2)∵点E是正方形内的抛物线上的动点, ∴设点E的坐标为(m,﹣![]() +2m)(0<m<4),
+2m)(0<m<4),
∴S△OAE+SOCE=![]() OAyE+
OAyE+![]() OCxE=﹣m2+4m+2m=﹣(m﹣3)2+9,
OCxE=﹣m2+4m+2m=﹣(m﹣3)2+9,
∴当m=3时,△OAE与△OCE面积之和最大,最大值为9.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目