题目内容
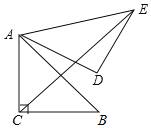
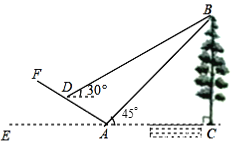
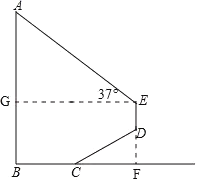
【题目】如图，某数学活动小组为测量学校旗杆AB的高度，沿旗杆正前方
米处的点C出发，沿坡角为30°的斜坡CD前进4米到达点D，在点D处安置测角仪，测得旗杆顶部A的仰角为37°，量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内，AB⊥BC，AB∥DE.求旗杆AB的高度.（参考数据：sin37°≈
，cos37°≈
，tan37°≈
，计算结果保留根号）
【答案】AB＝
.
【解析】
过点E作EG⊥AB于点G，延长ED交BC延长线于点F，则∠CFD＝90°，在Rt△CDF中求得DF=2， CF＝
，可得GE＝BF＝
，GB＝EF＝3.5，再求出AG＝GEtan∠AEG＝
，可得答案.
解：如图，过点E作EG⊥AB于点G，延长ED交BC延长线于点F，则∠CFD＝90°，
∵∠DCF＝30°，
∵CD＝4，∴DF=2， CF＝
＝，
∴BF＝BC＋CF＝
，
则GE＝BF＝，
GB＝EF＝ED＋DF＝1.5＋2＝3.5，
又∵∠AEG＝37°，
∴AG＝GEtan∠AEG＝tan37°=，
则AB＝AG＋BG＝
，
故旗杆AB的高度为（）米．
练习册系列答案
相关题目
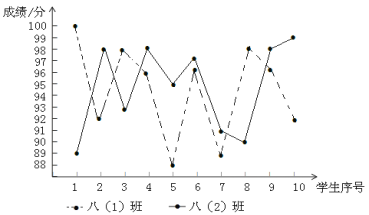
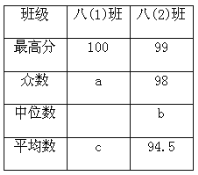
【题目】为了解某市市民“绿色出行”方式的情况，某校数学兴趣小组以问卷调查的形式，随机调查了某市部分出行市民的主要出行方式（参与问卷调查的市民都只从以下五个种类中选择一类），并将调查结果绘制成如下不完整的统计图．
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |
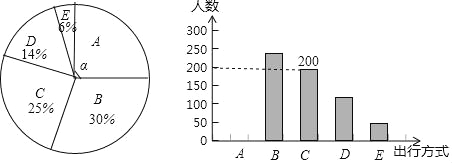
根据以上信息，回答下列问题：
（1）参与本次问卷调查的市民共有 人，其中选择B类的人数有 人；
（2）在扇形统计图中，求A类对应扇形圆心角α的度数，并补全条形统计图；
（3）该市约有12万人出行，若将A，B，C这三类出行方式均视为“绿色出行”方式，请估计该市“绿色出行”方式的人数．
