题目内容
【题目】如图![]() ,在平面直角角坐标系中,已知抛物线
,在平面直角角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点.
两点.
(1)求抛物线的函数表达式;
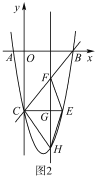
(2)如图![]() ,
,![]() 轴与抛物线相交于点
轴与抛物线相交于点![]() ,点
,点![]() 是直线
是直线![]() 下方抛物线上的动点,过点
下方抛物线上的动点,过点![]() 且与
且与![]() 轴平行的直线与
轴平行的直线与![]() ,
,![]() 分别交于点
分别交于点![]() 试探究当点
试探究当点![]() 运动到何处时,线段
运动到何处时,线段![]() 的最长,求点
的最长,求点![]() 的坐标;
的坐标;
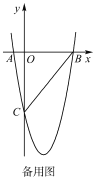
(3)若点![]() 为抛物线的顶点,点
为抛物线的顶点,点![]() 是该抛物线上的一点,在
是该抛物线上的一点,在![]() 轴、
轴、![]() 轴上分别找点
轴上分别找点![]() ,使四边形
,使四边形![]() 的周长最小,请求出点
的周长最小,请求出点![]() 的坐标.
的坐标.
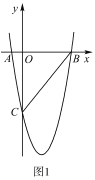
【答案】(1)y=x2-4x-5;(2)H(![]() ,
,![]() );(3)P、Q的坐标分别为P(
);(3)P、Q的坐标分别为P(![]() ,0),Q(0,
,0),Q(0,![]() ).
).
【解析】
(1)待定系数法,将点A、B代入抛物线解析式即可求出解析式.
(2)设点H、F的坐标,表示线段HF,将得到的关系式配方,配成顶点式就可以求出点H的坐标.
(3)利用对称性找到点P、Q的位置,进而求出点P、Q的坐标.
解:(1)由已知得![]()
把![]() 代入
代入![]() 得
得![]() ,
,
解得![]()
∴二次函数的表达式为y=x2-4x-5.
(2)设![]()
设直线![]() 的表达式为
的表达式为![]() ,解得
,解得![]()
![]() 直线
直线![]() 的表达式为
的表达式为![]()
![]()
![]()
![]()
(3)如图,分别作![]() 关于
关于![]() 轴,
轴,![]() 轴对称的点
轴对称的点![]() ,分别交
,分别交![]() 延长线于点
延长线于点![]()

![]() 点
点![]() 为顶点
为顶点
![]()
![]() 点
点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 的坐标为
的坐标为![]()
∵![]()
![]()
![]() 点
点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 的坐标为
的坐标为![]() ,
,
设直线![]() 的表达式为
的表达式为![]() ,
,
解得 ,
,
![]() 直线
直线![]() 的表达式为
的表达式为![]()
易知图中点![]() 即为符合条件的点
即为符合条件的点
∴P、Q的坐标分别为P(![]() ,0),Q(0,
,0),Q(0,![]() ).
).

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目