题目内容
【题目】如图,在平面直角坐标系中,已知抛物线y=![]() x2+
x2+![]() x-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线l经过A,C两点,连接BC.
x-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线l经过A,C两点,连接BC.
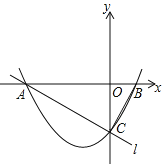
(1)求直线l的解析式;
(2)若直线x=m(m<0)与该抛物线在第三象限内交于点E,与直线l交于点D,连接OD.当OD⊥AC时,求线段DE的长;
(3)取点G(0,-1),连接AG,在第一象限内的抛物线上,是否存在点P,使∠BAP=∠BCO-∠BAG?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x2;(2)
x2;(2)![]() ;(3)P(
;(3)P(![]() ,
,![]() )
)
【解析】
(1)根据题目中的函数解析式可以求得点A和点C的坐标,从而可以求得直线l的函数解析式;
(2)根据题意作出合适的辅助线,利用三角形相似和勾股定理可以解答本题;
(3)根据题意画出相应的图形,然后根据锐角三角函数可以求得∠OAC=∠OCB,然后根据题目中的条件和图形,利用锐角三角函数和勾股定理即可解答本题.
(1)∵抛物线y=![]() x2+
x2+![]() x-2,
x-2,
∴当y=0时,得x1=1,x2=-4,当x=0时,y=-2,
∵抛物线y=![]() x2+
x2+![]() x-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,
x-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,
∴点A的坐标为(-4,0),点B(1,0),点C(0,-2),
∵直线l经过A,C两点,设直线l的函数解析式为y=kx+b,
![]() ,得
,得 ,
,
即直线l的函数解析式为y=![]() x2;
x2;
(2)直线ED与x轴交于点F,如图1所示,
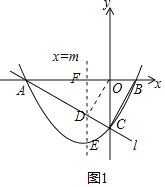
由(1)可得,
AO=4,OC=2,∠AOC=90°,
∴AC=2![]() ,
,
∴OD=![]() ,
,
∵OD⊥AC,OA⊥OC,∠OAD=∠CAO,
∴△AOD∽△ACO,
∴![]() ,
,
即![]() ,得AD=
,得AD=![]() ,
,
∵EF⊥x轴,∠ADC=90°,
∴EF∥OC,
∴△ADF∽△ACO,
∴![]() ,
,
解得,AF=![]() ,DF=
,DF=![]() ,
,
∴OF=4-![]() =
=![]() ,
,
∴m=-![]() ,
,
当m=-![]() 时,y=
时,y=![]() ×(
×(![]() )2+
)2+![]() ×(-
×(-![]() )-2=-
)-2=-![]() ,
,
∴EF=![]() ,
,
∴DE=EF-FD=![]()
![]() =
=![]() ;
;
(3)存在点P,使∠BAP=∠BCO-∠BAG,
理由:作GM⊥AC于点M,作PN⊥x轴于点N,如图2所示,

∵点A(-4,0),点B(1,0),点C(0,-2),
∴OA=4,OB=1,OC=2,
∴tan∠OAC=![]() ,tan∠OCB=
,tan∠OCB=![]() ,AC=2
,AC=2![]() ,
,
∴∠OAC=∠OCB,
∵∠BAP=∠BCO-∠BAG,∠GAM=∠OAC-∠BAG,
∴∠BAP=∠GAM,
∵点G(0,-1),AC=2![]() ,OA=4,
,OA=4,
∴OG=1,GC=1,
∴AG=![]() ,
,
![]() ,即
,即![]() ,
,
解得,GM=![]() ,
,
∴AM=![]() ,
,
∴tan∠GAM=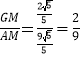 ,
,
∴tan∠PAN=![]() ,
,
设点P的坐标为(n,![]() n2+
n2+![]() n-2),
n-2),
∴AN=4+n,PN=![]() n2+
n2+![]() n-2,
n-2,
∴![]() ,
,
解得,n1=![]() ,n2=-4(舍去),
,n2=-4(舍去),
当n=![]() 时,
时,![]() n2+
n2+![]() n-2=
n-2=![]() ,
,
∴点P的坐标为(![]() ,
,![]() ),
),
即存在点P(![]() ,
,![]() ),使∠BAP=∠BCO-∠BAG.
),使∠BAP=∠BCO-∠BAG.