题目内容
(8分)如图,在□ABCD中,点E、F是对角线BD上的两点,且BE=DF.
 求证:(1)△ABE≌△CDF;(2)AE∥CF.
求证:(1)△ABE≌△CDF;(2)AE∥CF.
 求证:(1)△ABE≌△CDF;(2)AE∥CF.
求证:(1)△ABE≌△CDF;(2)AE∥CF.(证明略)
专题:证明题.
分析:根据平行四边形对边平行且相等的性质得到AB∥CD且AB=CD,所以∠ABE=∠CDF,所以两三角形全等;根据全等三角形对应角相等得到∠AEB=∠CFD,所以它们的邻补角相等,根据内错角相等,两直线平行即可得证.
解答:证明:(1)在□ABCD中,AB∥CD且AB=CD,
∴∠ABE=∠CDF,
在△ABE和△CDF中,
 ,
,∴△ABE≌△CDF(SAS);
(2)∵△ABE≌△CDF,
∴∠AEB=∠CFD(全等三角形对应角相等),
∴∠AEF=∠CFE(等角的补角相等),
∴AE∥CF(内错角相等,两直线平行).
点评:本题利用平行四边形的性质和三角形全等的判定求解,熟练掌握性质和判定定理并灵活运用是解题的关键.

练习册系列答案
相关题目
 被两条与边平行的线段
被两条与边平行的线段 分割成四个小矩形,
分割成四个小矩形, 与
与 交于点
交于点 .
.
 ,证明:
,证明: ;
; ,证明:
,证明: ;
; 的周长为1,求矩形
的周长为1,求矩形 的面积.
的面积.

 cm
cm
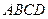 中,
中,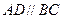 ,
,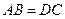 ,
,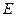 为
为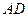 中点,连接
中点,连接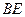 ,
,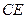 .
.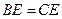 ;
;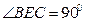 ,过点
,过点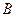 作
作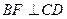 ,垂足为点
,垂足为点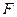 ,交
,交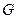 ,连接
,连接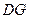 .
.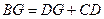 .
.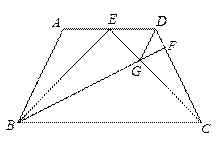
 ,则菱形较短的对角线长是( )
,则菱形较短的对角线长是( )


 ,E是DC上一点,且BE = BC,则DE的长为
,E是DC上一点,且BE = BC,则DE的长为