题目内容
平行四边形一边长为10,一条对角线长为6,则它的另一条对角线长b的取值范围为 .
14<b<26
由平行四边形的对角线互相平分,根据三角形三边之间的关系,可先求得另一对角线的一半的取值范围,进而可求出这条对角线的范围.
解:如图,已知平行四边形中,AB=10,AC=6,
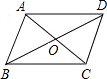
由题意得,BD=2OB,AC=2OA=6,
∴OB=1/2BD,OA=3,
∴在△AOB中,AB-OA<OB<AB+OA,可得7<OB<13,
即:14<BD<26,
故答案为:14<x<26.
解:如图,已知平行四边形中,AB=10,AC=6,

由题意得,BD=2OB,AC=2OA=6,
∴OB=1/2BD,OA=3,
∴在△AOB中,AB-OA<OB<AB+OA,可得7<OB<13,
即:14<BD<26,
故答案为:14<x<26.

练习册系列答案
相关题目

 B、
B、 C、
C、 D、
D、

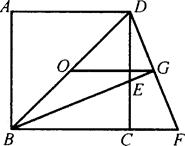
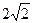 ,求正方形ABCD的面积.
,求正方形ABCD的面积.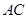 为正方形
为正方形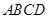 的对角线,
的对角线,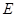 为
为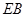 ,
,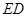 ,当
,当 时,
时,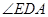 的度数为( )
的度数为( )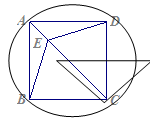
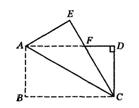
 求证:(1)△ABE≌△CDF;(2)AE∥CF.
求证:(1)△ABE≌△CDF;(2)AE∥CF.