题目内容
如图，在等腰梯形ABCD中，AB∥CD， 对角线AC⊥BC，∠B＝60º，BC＝2cm，则梯形ABCD的面积为（ ）
A．3 cm | B．6 cm | C．6cm | D．12 cm |
A
过点C作CE⊥AB，
∵AC⊥BC，∠B=60°，
∴∠CAB=30°，
∵BC=2cm，
∴AB=4cm，AC=2cm，
∴CE=cm，
∵梯形ABCD是等腰梯形，CD∥AB，
∴∠B=∠DAB=60°，∠CAB=∠DCA=30°，
∵∠CAB=30°，
∴∠DAC=∠DCA=30°，
∴CD=AD=BC=2cm，
∴梯形ABCD的面积=1/2
（AB+CD）×CE=1/2（4+2）×
=3cm2，
故选A．
∵AC⊥BC，∠B=60°，
∴∠CAB=30°，
∵BC=2cm，
∴AB=4cm，AC=2
cm，∴CE=
cm，∵梯形ABCD是等腰梯形，CD∥AB，
∴∠B=∠DAB=60°，∠CAB=∠DCA=30°，
∵∠CAB=30°，
∴∠DAC=∠DCA=30°，
∴CD=AD=BC=2cm，
∴梯形ABCD的面积=1/2
（AB+CD）×CE=1/2（4+2）×
=3
cm2，故选A．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
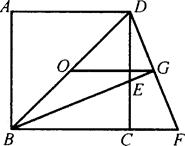
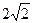，求正方形ABCD的面积．
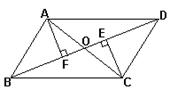
求证：(1)△ABE≌△CDF；(2)AE∥CF．
圃. 问矩形苗圃的一边长为多少时面积最大，最大面积是多少？
是四边形
的对角线
上两点，
．
．
