��Ŀ����
����Ŀ���۲��±���
��� | 1 | 2 | 3 | �� |
ͼ�� |
|
|
| �� |
���ǰ�ij������ĸ�����õ��Ķ���ʽ��Ϊ��������ʽ�����磺
��1�������������ʽ��Ϊ![]() ��
��
��2�������������ʽ��Ϊ![]() ��
��
�ش��������⣺
��1����3�������������ʽ��Ϊ________________��
��4�������������ʽ��Ϊ______________________��
��![]() �������������ʽ��Ϊ___________________��
�������������ʽ��Ϊ___________________��
��2������1�������������ʽ����ֵΪ![]() ����2�������������ʽ����ֵΪ
����2�������������ʽ����ֵΪ![]() ����
����![]() ��ֵ��
��ֵ��
��3���ڣ�2���������£���![]() �����������ʽ��ֵΪ
�����������ʽ��ֵΪ![]() ����ֱ��д��
����ֱ��д��![]() ��ֵ����û�У���˵�����ɣ�
��ֵ����û�У���˵�����ɣ�
���𰸡���1��![]() ��
��![]() ��
��![]() ����2��
����2��![]() ��
��![]() ����3��
����3��![]() ��
��![]() ��
��
��������
��1��������֪������x��y�����仯���ɵó���2�������������ʽ���Լ���n�������������ʽ����
��2�����ã�1��������ó�����x��y�ĵ�ʽ��ɷ���������𰸣�
��3�����ö��κ�����ֵ�ó��𰸣�
�⣺��1����3�������������ʽ��Ϊ��16x+9y��
��4�������������ʽ��Ϊ��25x+16y��
��n�������������ʽ��Ϊ��![]() ��
��
�ʴ�Ϊ��16x+9y��25x+16y��![]()
��2���ߵ�1�������������ʽ����ֵΪ-10����2�������������ʽ����ֵΪ-16��
���������ɵã�
![]() ����ã�
����ã�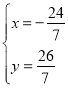
��x��y��ֵ�ֱ�Ϊ��![]() ��
��![]() ��
��
��3���ɣ�2����֪![]() ��
��![]()
���n�������������ʽ��Ϊ��![]()
��������ɵ�![]()
������![]()
��ã�![]() ��
��![]() ��
��