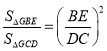题目内容
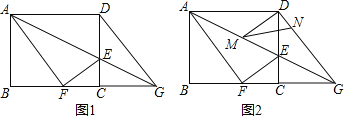
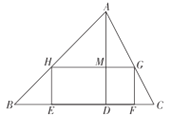
【题目】如图所示，要在底边BC=160cm，高AD=120cm的△ABC铁皮余料上，截取一个矩形EFGH，使点H在AB上，点G在AC上，点E，F在BC上，AD交HG于点M.
(1)设矩形EFGH的长HG=ycm，宽HE=xcm.求y与x的函数关系式；
(2)当x为何值时，矩形EFGH的面积S最大?最大值是多少?
【答案】（1）
；（2）当x=60时，S最大，最大为4800cm.
【解析】
（1）根据矩形的性质可得△AHG∽△ABC，根据相似三角形的性质即可得答案；（2）利用S=xy，把
代入得S关于x的二次函数解析式，根据二次函数的性质求出最大值即可.
解：(1)∵四辺形EFGH是矩形，
∴HG∥BC
∴ΔAHG∽ΔABC
∴
，即
∴
(2)把带入S=xy，
得
=
当x=60时，S最大，最大为4800cm.
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
【题目】某校为了解中学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况，随机抽取了
名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目)，并将调查结果绘制成如图统计图表：
节目 | 人数(名) | 百分比 |
最强大脑 |
|
|
朗读者 |
|
|
中国诗词大会 |
|
|
出彩中国人 |
|
|
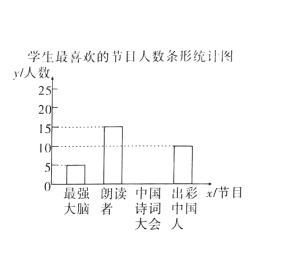
根据以上提供的信息．解答下列问题：
，
，
；
补全上面的条形统计图；
名女同学．其余为男同学，现要从中随机抽取
名同学代表学校参加市里组织的竞赛活动，请求出所抽取的名同学恰好是
名男同学和名女同学的概率．