题目内容
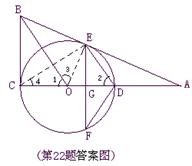
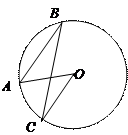
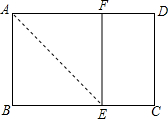
(8分)如图,⊙O的圆心在Rt△ABC的直角边AC上,⊙O经过C、D两点,与斜边AB交于点E,连结BO、ED,有BO∥ED,作弦EF⊥AC于G,连结DF.
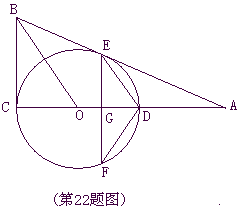
(1)求证:AB为⊙O的切线;
(2)若⊙O的半径为5,sin∠DFE=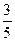 ,求EF的长.
,求EF的长.

(1)求证:AB为⊙O的切线;
(2)若⊙O的半径为5,sin∠DFE=
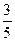 ,求EF的长.
,求EF的长.(1)略
(2)
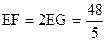
(1)证明:连结OE
∵ED∥OB
∴∠1=∠2,∠3=∠OED,
又OE=OD
∴∠2=∠OED
∴∠1=∠3 (1分)
又OB="OB " OE= OC
∴△BCO≌△BEO(SAS) (2分)
∴∠BEO=∠BCO=90° 即OE⊥AB
∴AB是⊙O切线. (4分)
(2)解:∵∠F=∠4,CD=2·OC=10;由于CD为⊙O的直径,∴在Rt△CDE中有:
ED=CD·sin∠4=CD·sin∠DFE=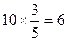 (5分)
(5分)
∴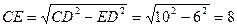 (6分)
(6分)
在Rt△CEG中,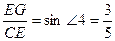
∴EG=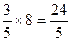 (7分)
(7分)
根据垂径定理得: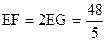 (8分)
(8分)

∵ED∥OB
∴∠1=∠2,∠3=∠OED,
又OE=OD
∴∠2=∠OED
∴∠1=∠3 (1分)
又OB="OB " OE= OC
∴△BCO≌△BEO(SAS) (2分)
∴∠BEO=∠BCO=90° 即OE⊥AB
∴AB是⊙O切线. (4分)
(2)解:∵∠F=∠4,CD=2·OC=10;由于CD为⊙O的直径,∴在Rt△CDE中有:
ED=CD·sin∠4=CD·sin∠DFE=
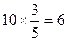 (5分)
(5分)∴
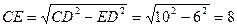 (6分)
(6分)在Rt△CEG中,
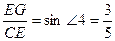
∴EG=
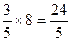 (7分)
(7分)根据垂径定理得:
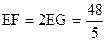 (8分)
(8分)
练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
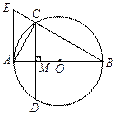
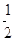
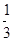
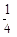
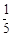
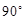 ,半径为
,半径为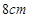 的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计).该圆锥底面圆的半径为
的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计).该圆锥底面圆的半径为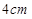

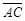 交于另一点D。若A=70,B=60,则
交于另一点D。若A=70,B=60,则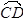 的度数为何?
的度数为何?