题目内容
(本题满分10分,每小题5分)
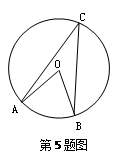
如图,AB为⊙O的直径,弦CD⊥AB,垂足为点M,AE切⊙O于点A,交BC的延长线于点E,连接AC.
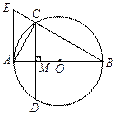
(1)若∠B=30°,AB=2,求CD的长;
(2)求证:AE2=EB·EC.
如图,AB为⊙O的直径,弦CD⊥AB,垂足为点M,AE切⊙O于点A,交BC的延长线于点E,连接AC.
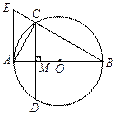
(1)若∠B=30°,AB=2,求CD的长;
(2)求证:AE2=EB·EC.
(1)
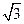
(2)证明略
解:(1)解法一: 解法二:
∵AB为⊙O的直径, ∵AB为⊙O的直径,∠B=30°,
∴∠ACB=90°.……1分 ∴AC=
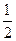 AB=1,BC=AB•cos30°=
AB=1,BC=AB•cos30°=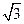 …2分
…2分∵在Rt△ABC中,∠B=30°,AB=2, ∵弦CD⊥直径AB于点M,
∴BC=AB•cos30°=2×
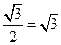 …2分 ∴CD=2CM,AB×CM=AC×BC……4分
…2分 ∴CD=2CM,AB×CM=AC×BC……4分 ∵弦CD⊥直径AB,∠B=30°, ∴CD=2CM=2×
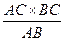
∴ CM=
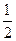 BC=
BC=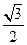 .……4分 =2×
.……4分 =2×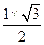 =
=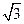 ……5分
……5分CD=2CM=
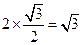 .……5分
.……5分 (其它解法请酌情给分)
(2)证明:∵AE切⊙O于点A,AB为⊙O的直径,
∴∠BAE=90°,∠ACE=∠ACB=90°, 6分
∴∠ACE=∠BAE=90°. 7分
又∵∠E=∠E,
∴Rt△ECA∽Rt△EAB. 8分
∴
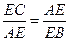 . 9分
. 9分∴AE2=EB•EC. 10分

练习册系列答案
相关题目

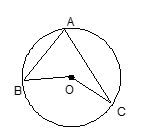
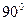 ,BC为⊙O的直径, AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.
,BC为⊙O的直径, AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.
 ,求⊙O的直径BC.
,求⊙O的直径BC.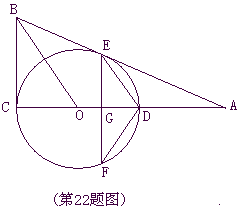
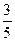 ,求EF的长.
,求EF的长.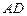 为
为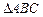 外接圆的直径,
外接圆的直径,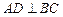 ,垂足为点
,垂足为点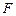 ,
,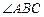 的平分线交
的平分线交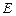 ,连接
,连接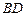 ,
,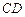 .
.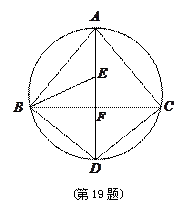
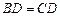 ;
; 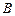 ,
,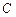 三点是否在以
三点是否在以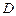 为圆心,以
为圆心,以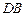 为半径的圆上?并说明理由.
为半径的圆上?并说明理由.