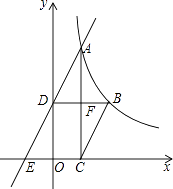Question

【题目】已知△ABC是等腰直角三角形，∠A=90°，D是腰AC上的一个动点，过C作CE垂直于BD的延长线，垂足为E，如图1

（1）求证：ADCD=BDDE；
（2）若BD是边AC的中线，如图2，求 的值；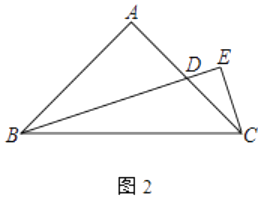

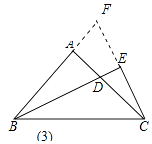
（3）如图3，连接AE．若AE=EC，求 的值．

Answer 1

【答案】
（1）

解：∵CE⊥BD，

∴∠A=∠E=90°，

∵∠ADB=∠EDC，

∴△BAD∽△CED，

∴ ，

∴ADCD=BDDE；

（2）

解：设CD=AD=a，则AB=AC=2a．

在Rt△ABD中，由勾股定理得：BD= a，

由（1）知，△BAD∽△CED，

∴ ，

∴ ，

解得：CE= a，

∴ = = ；

（3）

解：如图3，延长CE、BA相交于点F．

∵BE是∠ABC的角平分线，且BE⊥CF

在△BEC和△BEF中， ，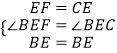

∴△BEC≌△BEF，

∴CE=EF，

∴CF=2CE

又∵∠ABD+∠ADB=∠CDE+∠ACF=90°，

且∠ADB=∠CDE，

∴∠ABD=∠ACF

∵AB=AC，∠BAD=∠CAF=90°，

在△ABD和△ACF中， ，

∴△ABD≌△ACF（ASA），

∴BD=CF，

∴BD=2CE，

∴ =2．

【解析】（1）直接判断出△ABD∽△ECD，即可得出结论；（2）先设AB=AC=2a，CD=a，则BC= a，AD=a．求出BD，而△BAD∽△CED，得出 ，代入求出CE即可解决问题．（2）如图3，延长CE、BA相交于点F．只要证明△BEC≌△BEF，推出CE=EF，CF=2CE，由ABD≌△ACF，推出BD=CF，即可解决问题．
【考点精析】本题主要考查了勾股定理的概念和相似三角形的判定与性质的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方才能正确解答此题．