题目内容
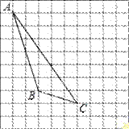
【题目】如图,在方格纸内将△ABC水平向右平移4个单位,再向下后平移1得到△A′B′C′.
(1)画出平移后的△A′B′C′;
(2)画出AB边上的高线CD(利用三角板画图);
(3)画出△ABC中AB边上的中线CE;
(4)图中AC与A′C′的关系是: ;
(5)△BCE的面积为 .
(6)若△A″BC的面积与△ABC面积相同,则A″(A″在格点上)的位置(除A点外)共有_________个.
【答案】(1)(2)(3)略(4)平行且相等(5)4(6)3
【解析】
(1)分别作出点A、B、C向右平移4个单位,再向下后平移1得到的对应点,顺次连接即可得;
(2)根据三角形高的定义作出线段可得;
(3)根据三角形中线的定义作出线段可得;
(4)根据平移的性质即可得;
(5)利用割补法求解可得;
(6)根据两三角形的底边公共,而面积相等知点A″应位于过点A且平行于BC的直线上,据此可得.
(1)如图,△A′B′C′即为所求;

(2)如图,线段CD即为所求;
(3)如图,线段CE即为所求;
(4)图中AC与A′C′平行且相等,
故答案为:平行且相等;
(5)S△BCE=![]() ×4×4-
×4×4-![]() ×1×3-1×1-
×1×3-1×1-![]() ×1×3=4;
×1×3=4;
(6)若△A″BC的面积与△ABC面积相同,
则点A″应位于过点A且平行于BC的直线上,由图可知,这样的格点A″共有3个,
故答案为:3.

 字词句段篇系列答案
字词句段篇系列答案【题目】某足球协会举办了一次足球联赛,其记分规定及奖励方案如下表:
胜一场 | 平一场 | 负一场 | |
积分 | 3 | 1 | 0 |
奖金(元/人) | 1300 | 500 | 0 |
当比赛进行到第11轮结束(每队均须比赛11场)时,A队共积17分,每赛一场,每名参赛队员均得出场费300元.设A队其中一名参赛队员所得的奖金与出场费的和为w(元).
(1)试说明w是否能等于11400元.
(2)通过计算,判断A队胜、平、负各几场,并说明w可能的最大值.