��Ŀ����
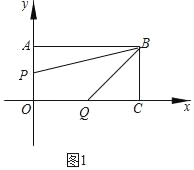
����Ŀ����ͼ��������AOCB�Ķ���A��m��n����C��p��q�����������ϣ���֪![]() ��
��![]() ���Ƿ���x+2y��4�������⣬��B�ڵ�һ�����ڣ�
���Ƿ���x+2y��4�������⣬��B�ڵ�һ�����ڣ�
��1�����B�����ꣻ
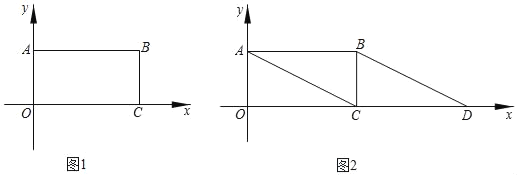
��2������P�ӵ�A������y�Ḻ���᷽����1����λÿ����ٶ��˶���ͬʱ��Q�ӵ�C��������x�Ḻ���᷽����2����λÿ����ٶ��˶������˶���������ʱ���ı���BPOQ���Ϊ������ABCO�����һ�룻
��3����ͼ2�����߶�AC��x��������ƽ�Ƶõ��߶�BD����E��a��b��Ϊ�߶�BD������һ�㣬����a+2b��ֵ�Ƿ�仯�����仯�����䷶Χ�������仯������ֵ����ֱ��д�����ۣ�
���𰸡���1����B������Ϊ��4��2������2���˶���1��ʱ���ı���BPOQ���Ϊ������ABCO�����һ�룻��3��a+2b��ֵ���仯��ֵΪ8.
��������
��1����������������ʰ�A,C���뷽��x+2y��4���õ��Ǹ������⣬�ٸ��ݾ��ε����ʼ��ɽ��.
��2����AP��t��CQ��2t���ٸ����ı���BPOQ�����������AOCB���������ABP���������BCQ��������t���ɽ��.
��3����EF��CD��F����ƽ�Ƶ���֤���ı���ABDC��ƽ���ı��Σ��ٸ���ƽ���ı��ε����ʵó�CD��AB��4��OD��OC+CD��8���ٸ��ݵ�E������Ϊ��a��b�����ó�OF��a��EF��b��DF��8��a������������������ε��ж������ʣ����ɽ��.
��1����A��m��n����C��p��q����
��m��0��n��0��p��0��q��0��
�߷���x+2y��4�ķǸ�������Ϊ![]() ��
��
��A��0��2����C��4��0����
���ı���AOCB�Ǿ��Σ�
��BC��OA��2��AB��OC��4��
���B��������4��2����
��2����ͼ1��ʾ��������ã�AP��t��CQ��2t��
���ı���BPOQ�����������AOCB���������ABP���������BCQ�������4��2��![]() ��4��t��
��4��t��![]() ��2t��2��
��2t��2��![]() ��4��2��
��4��2��
��ã�t��1��
���˶���1��ʱ���ı���BPOQ���Ϊ������ABCO�����һ�룻
��3��a+2b��ֵ���仯��ֵΪ8���������£�
��EF��CD��F����ͼ2��ʾ��
��EF��OA��BC��
��ƽ�Ƶ����ʵã�AC��BD��AC��BD��
���ı���ABDC��ƽ���ı��Σ�
��CD��AB��4��
��OD��OC+CD��8��
�ߵ�E������Ϊ��a��b����
��OF��a��EF��b��
��DF��8��a��
��EF��BC��
���DEF�ס�DBC��
��![]() ��
��
�����ã�a+2b��8��


����Ŀ��ϣ����ѧ���꼶ѧ����չ����ӻ��ÿ����5��ѧ���μӣ��������ܷ��������Σ��ڹ涨ʱ����ÿ����100�����ϣ���100��Ϊ�������±��dzɼ��Ϻõļװ���Ұ�5��ѧ���ı����ɼ�����λ������
1�� | 2�� | 3�� | 4�� | 5�� | ���� | |
�װ� | 100 | 98 | 110 | 89 | 103 | 500 |
�Ұ� | 89 | 100 | 95 | 119 | 97 | 500 |
��ͳ�Ʒ�������5��ѧ������ӵ��ܸ����������ʱ��ѧ�����飬����ͨ�����������е�������Ϣ��Ϊ�ο�������ش��������⣺
��1��������������ݵ���λ����
��2����������������ݵķ�����Ƚ���һ��С��
��3������������Ϣ������ΪӦ�ðѹھ���״������һ���ࣿ��������.