题目内容
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃，其中一边靠墙，另外三边用长为30米的篱笆围成．已知墙长为18米(如图所示)，设这个苗圃垂直于墙的一边长为x米．
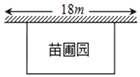
(1)若苗圃的面积为72平方米，求x的值；
(2)这个苗圃的面积能否是120平方米？请说明理由．
【答案】（1）x的值为12；（2）这个苗圃的面积不能是120平方米，理由见解析.
【解析】
（1）用x表示出矩形的长为30-2x，利用矩形面积公式建立方程求解，根据平行于墙的边长不能大于18米，舍去不符合题意的解；
（2）根据面积120平方米建立方程，若方程有解，则可以达到120平米，否则不能.
解：（1）根据题意得
，
化简得
，
或
∴
，
当
时，平行于墙的一边为30-2x=6＜18，符合题意；
当
时，平行于墙的一边为30-2x=24＞18，不符合题意，舍去.
故x的值为12.
（2）根据题意得
化简得
，∴方程无实数根
故这个苗圃的面积不能是120平方米.
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
【题目】为庆祝新中国成立70周年，并体现绿色节能理念，我市某工厂降低了某种工艺品的成本，两个月内从每件产品成本50元，降低到了每件32元，
（1）请问工厂平均每月降低率为多少？
（2）该工厂将产品投放市场进行实销，经过调查，得到如下数据：
销售单价 | …… | 40 | 50 | 60 | 70 | …… |
每天销售量 | …… | 400 | 300 | 200 | 100 | …… |
把上表中
、
的各组对应值作为点的坐标，在下面的平面直角坐标系中描出相应的点，猜想与的函数关系，并求出函数关系式.
（3）当销售单价定为多少时，工艺厂试销该工艺品每天活得的利润最大？最大利润是多少？
