题目内容
【题目】如图,在△ABC中,D,E分别是AB,AC上的点,∠AED=∠ABC,∠BAC的平分线AF交DE于点G,交BC于点F.
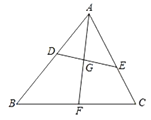
(1)试写出图中所有的相似三角形;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)△ABC∽△AED.△AEG∽△ABF.△ADG∽△ACF;(2)![]()
【解析】
(1)根据两组对应角相等可判断△ABC∽△AED,△ADG∽△ACF,△AEG∽△ABF.
(2)根据相似三角形的对应高相等可以进行计算.
解:(1)∵∠AED=∠ABC,∠EAD=∠BAC,
∴△ABC∽△AED,
∴∠ADE=∠ACB
∵∠AED=∠ABC,∠EAG=∠BAF,
∴△AEG∽△ABF.
∵∠EDG=∠ACF,∠DAG=∠CAF,
∴△ADG∽△ACF.
(2)∵![]() ,
,
∴![]() ,
,
∵由(1)可知△ABC∽△AED,
∴![]() ,
,
∵△ADG∽△ACF,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目
【题目】为庆祝新中国成立70周年,并体现绿色节能理念,我市某工厂降低了某种工艺品的成本,两个月内从每件产品成本50元,降低到了每件32元,
(1)请问工厂平均每月降低率为多少?
(2)该工厂将产品投放市场进行实销,经过调查,得到如下数据:
销售单价 | …… | 40 | 50 | 60 | 70 | …… |
每天销售量 | …… | 400 | 300 | 200 | 100 | …… |
把上表中![]() 、
、![]() 的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想
的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想![]() 与
与![]() 的函数关系,并求出函数关系式.
的函数关系,并求出函数关系式.
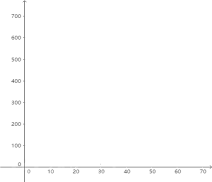
(3)当销售单价定为多少时,工艺厂试销该工艺品每天活得的利润最大?最大利润是多少?