Question

【题目】如图，已知正方形ABCD的边长为4，以AB为一边作等边△ABE，使点E落在正方形ABCD的内部，连接AC交BE于点F，连接CE、DE，则下列说法中：①△ADE≌△BCE；②∠ACE=30°；③AF=CF；④ =2+，其中正确的有（　　）

A. 1个 B. 2个 C. 3个 D. 4个

Answer 1

【答案】D

【解析】

根据正方形的性质，全等三角形的判定，可以证明①②正确，作FH⊥BC于H，设FH=CH=a，则BH=a，利用勾股定理求出a，即可判断③④正确；

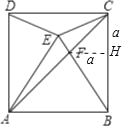
∵四边形ABCD是正方形，△AEB是等边三角形，

∴AD=AE=AB=BE=BC,∠DAB=∠CBA=90°,∠EAB=∠EBA=60°，

∴∠DAE=∠EBC=30°，

∴△ADE≌△BCE，故①正确，

∵∠BEC=∠BCE=(180°30°)=75°,∠ACB=45°，

∴∠ACE=∠BCE∠ACB=30°，故②正确，

作FH⊥BC于H,设FH=CH=a,则BH=3，

∵BC=4，

∴a+a=4，

∴a=22，

∴CF=a=22，

∵AC=4，

∴AF=AC=CF=62，

∴AF=CF，故③正确，

∵BF=2FH=44，

∴EF=BEBF=84，

∴S△BCES△ECF==2+，故④正确，

故选：D.