题目内容
【题目】如图,抛物线y=﹣x2+bx+c的图象与x轴交于A(﹣5,0),B(1,0)两点,与y轴交于点C,抛物线的对称轴与x轴交于点D.
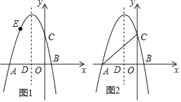
(1)求抛物线的函数表达式;
(2)如图1,点E(x,y)为抛物线上一点,且﹣5<x<﹣2,过点E作EF∥x轴,交抛物线的对称轴于点F,作EH⊥x轴于点H,得到矩形EHDF,求矩形EHDF周长的最大值;
(3)如图2,点P为抛物线对称轴上一点,是否存在点P,使以点P,A,C为顶点的三角形是直角三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2﹣4x+5.(2)![]() ;(3)P坐标为(﹣2,7)或(﹣2,﹣3)或(﹣2,6)或(﹣2,﹣1).
;(3)P坐标为(﹣2,7)或(﹣2,﹣3)或(﹣2,6)或(﹣2,﹣1).
【解析】试题分析:(1)利用待定系数法即可解决问题;
(2)构建二次函数利用二次函数的性质即可解决问题;
(3)分三种情形分别求解①当![]() 由
由![]() 列出方程即可解决.②当
列出方程即可解决.②当![]() 时,由
时,由![]() 列出方程即可解决.③当
列出方程即可解决.③当![]() 时,由
时,由![]() 列出方程即可;
列出方程即可;
试题解析:(1)把A(5,0),B(1,0)两点坐标代入![]()
得到![]()
解得![]()
∴抛物线的函数表达式为![]()
(2)如图1中,
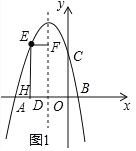
∵抛物线的对称轴x=2, ![]()
∴![]()
∴矩形EFDH的周长![]()
∵2<0,
∴![]() 时,矩形EHDF的周长最大,最大值为
时,矩形EHDF的周长最大,最大值为![]()
(3)如图2中,设P(2,m)
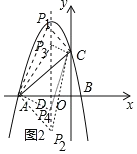
①当![]() ∵
∵![]()
∴![]()
解得m=7,
∴P1(2,7).
②当![]() 时,∵
时,∵![]()
∴![]()
解得m=3,
∴P2(2,3).
③当![]() 时,∵
时,∵![]()
∴![]()
解得m=6或1,
∴P3(2,6),P4(2,1),
综上所述,满足条件的点P坐标为(2,7)或(2,3)或(2,6)或(2,1).

【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数 | 1 | 2 | 3 | 4 | … |
碟子的高度(单位:cm) | 2 | 2+1.5 | 2+3 | 2+4.5 | … |
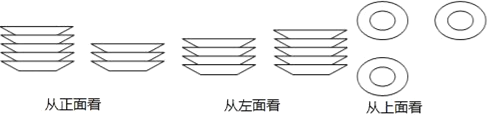
(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示).
(2)分别从正面、左面、上面三个方向看这些碟子,看到的形状图如图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.