题目内容
【题目】临近端午节,某食品店每天卖出300只粽子,卖出一只粽子的利润为1元.经调查发现,零售单价每降0.1元,每天可多卖出100只粽子.为了使每天获得的利润更多,该店决定把零售单价下降m(0<m<1)元,
(1)零售单价降价后,每只利润为 元,该店每天可售出 只粽子.
(2)在不考虑其他因素的条件下,当零售单价下降多少元时,才能使该店每天获取的利润是420元,且卖出的粽子更多?
【答案】(1) (1-m) ,(300+1000m);(2)当零售单价下降0.4元时,才能使该店每天获取的利润是420元,且卖出的粽子更多
【解析】
(1)降价后的利润等于原来的利润-降价即可得到;每天的销售量等于原有销售量加上增加的销售量即可;
(2)利用总利润等于销售量乘以每件的利润即可得到方程求解.
(1)该店每天可售出300+100×![]() =(300+1000m)只粽子.
=(300+1000m)只粽子.
每只利润为(1-m)元;
(2) 根据题意,得(1-m)(300+1000m)=420,
解得m1=0.4 m2=0.3,
显然,当m=0.4时, 300+1000m=700,
当 m=0.3时, 300+1000m=600,
700>600,
答:当零售单价下降0.4元时,才能使该店每天获取的利润是420元,且卖出的粽子更多.

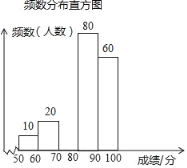
【题目】某校组织了全校1500名学生参加传统文化知识网络竞赛.赛后随机抽取了其中200名学生的成绩作为样本进行整理,并制作了如下不完整的频数分布表和频数分布直方图.
成绩(分) | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | n |
70≤x<80 | m | 0.15 |
80≤x<90 | 80 | 0.40 |
90≤x<100 | 60 | 0.30 |
请根据图表提供的信息,解答下列各题:
(1)表中m= ,n= ,请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段80≤x<90对应扇形的圆心角的度数是 ;
(3)若成绩在80分以上(包括80分)为合格,则参加这次竞赛的1500名学生中成绩合格的大约有多少名?