Question

【题目】在平面直角坐标系中，抛物线的的顶点为.

（1）顶点的坐标为 .

（2）横、纵坐标都是整数的点叫做整点.若轴且

①点的坐标为 ；

②过点作轴的垂线，若直线与抛物线交于两点，该抛物线在之间的部分与线段所围成的区域（包括边界）恰有七个整点，结合函数图象，求的取值范围.

Answer 1

【答案】（1）；（2）①或；②或

【解析】

（1）利用配方法即可解决问题；
（2）①m=1代入抛物线解析式，求出A、B两点坐标即可解决问题；
②根据题意画出图形，结合图形列出关于m的不等式，解之确定m的取值范围．

解：（1）∵y=mx2-4mx+4m-2=m（x-2）2-2，
∴抛物线顶点M的坐标（2，-2）．
故答案为：（2，-2）；
（2）①由题意可知：N（2，0）或（2，-4），
故答案为：（2，0）或（2，-4）；
②分两种情况：
①当N在点M的上方时，此时N在x轴上，即直线l与x轴重合，如图所示，抛物线在P、Q之间的部分与线段PQ所围成的区域（包括边界）恰有七个整点，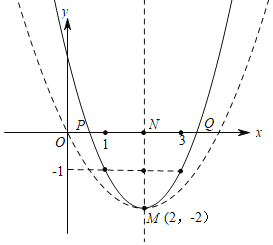

∴当x=1时，y≤-1，当x=0时，y＞0，
则 ，解得：＜m≤1；
②当N在点M的下方时，如图所示，抛物线在P、Q之间的部分与线段PQ所围成的区域（包括边界）恰有七个整点，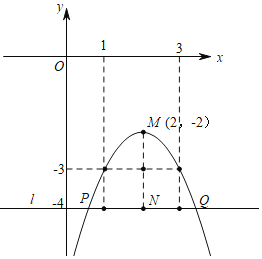

∴当x=1时，y≥-3，当x=0时，y＜-4，
则，解得：-1≤m＜-；
综上，m的取值范围是：＜m≤1或-1≤m＜．