题目内容
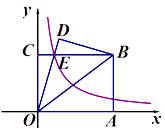
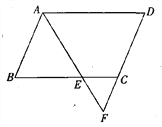
【题目】在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-1(m>0)与x轴的交点为A,B,顶点为C,将抛物线在A,C,B之间的部分记为图象E(A,B两点除外).
(1)求抛物线的顶点坐标.
(2)AB=6时,经过点C的直线y=kx+b(k≠0)与图象E有两个交点,结合函数的图象,求k的取值范围.
(3)若横、纵坐标都是整数的点叫整点.
①当m=1时,求线段AB上整点的个数;
②若抛物线在点A,C,B之间的图象E与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.
【答案】
(1)
C(1,-1).
(2)
AB=6时,抛物线与x轴的两个交点分别是(-2,0),(4,0),又因为顶点为(-1,1),当直线经过C与A,C与B时,分别解得k= ![]() ,所以k的取值范围为
,所以k的取值范围为 ![]() <k<0,或0<k<
<k<0,或0<k< ![]() .
.
(3)
①当m=1时,抛物线表达式为y=x2-2x,因此A、B的坐标分别为(0,0)和(2,0),则线段AB上的整点有(0,0),(1,0),(2,0)共3个.
②抛物线顶点为(1,-1),则指定区域的整点的纵坐标只能为-1或者0,所以即要求AB线段上(含AB两点)必须有5个整点;
令y=mx2-2mx+m-1=0,得到A、B两点坐标分别为( ![]() ,0),(
,0),( ![]() ,0),即5个整点是以(1,0)为中心向两侧分散,
,0),即5个整点是以(1,0)为中心向两侧分散,
进而得到2≤ ![]() <3,所以
<3,所以 ![]() <m≤
<m≤ ![]() .
.
【解析】(1)y=mx2-2mx+m-1=m(x-1)2-1,
则顶点C(1,-1).
(2)因为y=mx2-2mx+m-1=m(x-1)2-1,
所以对称轴为直线x=1,
因为AB=6,所以抛物线与x轴的两个交点分别是(-2,0),(4,0),
因为直线y=kx+b(k≠0)过C(1,-1)点,则y=kx-k-1,
当直线经过(-2,0)时,代入得-2k-k-1=0,
解得k=![]() ;
;
当直线经过(4,0)时,代入得4k-k-1=0,
解得k=![]() .
.
综上所述,因为图象E不包括A,B,则![]() <k<0,或0<k<
<k<0,或0<k< ![]() .
.
(3)①当m=1时,抛物线表达式为y=x2-2x,
因此A、B的坐标分别为(0,0)和(2,0),
则线段AB上的整点有(0,0),(1,0),(2,0)共3个.
②抛物线顶点为(1,-1),
则指定区域的整点的纵坐标只能为-1或者0,
所以即要求AB线段上(含AB两点)必须有5个整点;
令y=mx2-2mx+m-1=0,得到A、B两点坐标分别为( ![]() ,0),(
,0),( ![]() ,0),即5个整点是以(1,0)为中心向两侧分散,分别为(-1,0),(0,0),(1,0),(2,0),(3,0),
,0),即5个整点是以(1,0)为中心向两侧分散,分别为(-1,0),(0,0),(1,0),(2,0),(3,0),
则-2<![]() ≤-1,
≤-1,
进而得到2≤ ![]() <3,
<3,
所以 ![]() <m≤
<m≤ ![]() .
.
(1)根据顶点公式(![]() ),代入相应值计算即可或者配成顶点式;
),代入相应值计算即可或者配成顶点式;
(2)图象E指的是A,B,C之间所构成的图象,根据C(1.-1)可求出b,根据与图象E有两个交点可求出k的聚值范围;要理解当k>0时,随着k的增大,直线与x轴的正半轴的较小的夹角会越来越大;当k<0时,随着k的增大,直线与x轴的正半轴的较小的夹角会越来越小;
(3)①根据m的值可求出A,B的坐标,即可得到线段AB的整点坐标,包括A点和B点;
②因为二次函数的最小值是-1,而在抛物线在点A,C,B之间的图象E与线段AB所围成的区域内(包括边界)中是-1≤y<0的,除了(1,-1),所以其他整点一定在线段AB上.

 名题金卷系列答案
名题金卷系列答案【题目】观察下列一组勾股数:
|
|
| |
第1组 | 3=2×1+1 | 4=2×1×(1+1) | 5=2×1×(1+1)+1 |
第2组 | 5=2×2+1 | 12=2×2×(2+1) | 13=2×2×(2+1)+1 |
第3组 | 7=2×3+1 | 24=2×3×(3+1) | 25=2×3×(3+1)+1 |
第4组 | 9=2×4+1 | 40=2×4×(4+1) | 41=2×4×(4+1)+1 |
… | … | … | … |
观察以上各组勾股数的特点:
(1)请写出第7组勾股数![]() ,
,![]() ,
,![]() ;
;
(2)写出第![]() 组勾股数
组勾股数![]() ,
,,
![]() .
.