题目内容
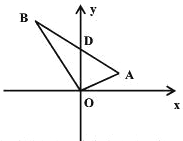
【题目】如图,直角三角形OAB中,∠AOB=90°,∠A=60°∠xOA=30°,AB与y轴的交点坐标D为(0,4)。求A、B的坐标.
【答案】点A的坐标为(2![]() ,2);点B的坐标为:(-2
,2);点B的坐标为:(-2![]() ,6).
,6).
【解析】分析:首先过点A作AC⊥x轴于点C,由直角三角形OAB中,∠AOB=90°,∠A=60°,∠BOD=30°,易得△AOD是等边三角形,即可求得OA的长,然后由含30°角的直角三角形的性质,求得AC的长,由勾股定理即可求得OC的长,则可求得答案.
详解:
过点A作AC⊥x轴于点C,

∵直角三角形OAB中,∠AOB=90°,∠A=60°,∠BOD=30°,
∴∠AOD=∠AOB-∠BOD=60°,
∴∠AOD=∠A,
∴OA=OD,
∴△AOD是等边三角形,
∵点D的坐标为(0,4),
∴OA=OD=4,
∵∠AOC=90°-∠AOD=30°,
∴AC=![]() OA=2,
OA=2,
∴OC=![]() ,
,
∴点A的坐标为:(2![]() ,2).
,2).
同理可得,点B的坐标为:(-2![]() ,6).
,6).

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案【题目】某校组织了一次G20知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题: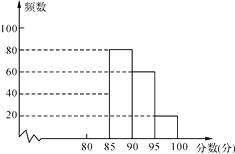
分数段 | 频数 | 频率 |
80≤x<85 | a | 0.2 |
85≤x<90 | 80 | b |
90≤x<95 | 60 | c |
95≤x<100 | 20 | 0.1 |
(1)求出表中a,b,c的数值,并补全频数分布直方图;
(2)获奖成绩的中位数落在哪个分数段?
(3)估算全体获奖同学成绩的平均分.
【题目】学生每天锻炼一小时,某校开展了形式多样的体育活动项目,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的频率统计表和频数分布直方图.请你根据图表信息完成下列各题:
运动项目 | 频数(人数) | 频率 |
篮球 | 20 | 0.40 |
乒乓球 | n | 0.10 |
足球 | 10 | m |
其他 | 15 | 0.30 |
合计 | a | 1.00 |
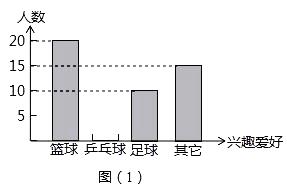
(1)填空: a=;m=;n=;
(2)请将条形统计图补充完整;
(3)该校共有学生1500人,估计参加乒乓球项目的学生有人;
【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | ||
5≤x<6 | 10 | 20% |
6≤x<7 | 12% | |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |

(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.