题目内容
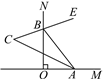
【题目】如图所示,已知CE⊥AB于点E,BD⊥AC于点D,BD与CE交于点O,且AO平分∠BAC.
(1)图中有多少对全等三角形?请你一一列举出来(不要求说明理由).
(2)小明说:欲说明BE=CD,可先说明△AOE≌△AOD得到AE=AD,再说明△ADB≌△AEC得到AB=AC,然后利用等式的性质即可得到BE=CD,请问他的说法正确吗?如果不正确,请说明理由;如果正确,请按他的思路写出推导过程.
(3)要得到BE=CD,你还有其他的思路吗?请仿照小明的说法具体说一说你的想法.

【答案】(1)见解析;(2)正确,理由见解析.
【解析】
(1)根据全等三角形的判定得出即可.
(2)求出∠EAO=∠DAO,∠AEO=∠ADO=90°,根据AAS证△AEO≌△ADO,推出AE=AD,根据ASA证△ADB≌△AEC,推出AB=AC即可.
(3)根据垂直和角平分线性质得出OE=OD,∠BEO=∠CDO=90°,根据ASA推出△BEO≌△CDO即可.
(1)共4对,分别是△AOE≌△AOD,△BOE≌△COD,△AOB≌△AOC,△ABD≌△ACE.
(2)正确.
因为CE⊥AB于点E,BD⊥AC于点D,
所以∠AEO=∠ADO.
因为AO平分∠BAC,
所以∠OAE=∠OAD.
在△AOE和△AOD中,
因为∠AEO=∠ADO,∠OAE=∠OAD,AO=AO,
所以△AOE≌△AOD,
所以AE=AD.
在△ADB和△AEC中,
因为∠BAD=∠CAE,AD=AE,∠ADB=∠AEC,
所以△ADB≌△AEC,
所以AB=AC,
所以AB-AE=AC-AD,
即BE=CD.
(3)答案不唯一,如可先说明△AOE≌△AOD,得到OE=OD,再说明△BOE≌△COD,得到BE=CD.

练习册系列答案
相关题目