题目内容
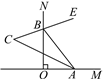
【题目】如图,∠MON=90°,点A,B分别在射线OM,ON上运动,BE平分∠ABN,BE的反向延长线与∠BAO的平分线交于点C.
(1)当点A,B移动后,∠BAO=45°时,∠C=________;
(2)当点A,B移动后,∠BAO=60°时,∠C=________;
(3)由(1)(2)猜想∠C是否随点A,B的移动而发生变化,并说明理由.
【答案】(1)(1)45°;(2)45°;(3)∠C不随点A,B的移动而发生变化,理由详见解析.
【解析】
(1)根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠ABN, 再根据角平分线的定义求出∠ABE和∠BAC, 然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解;
(2)与(1)方法相同求解可得答案;
(3)与(1)的思路相同解答可得答案.
解:(1)根据三角形的外角性质,
∠ABN=∠AOB+∠BAO=90![]() +45
+45![]() =135
=135![]()
![]() BE平分∠ABN,AC平分∠BAO,
BE平分∠ABN,AC平分∠BAO,
![]() ∠ABE=
∠ABE=![]() ∠ABN=67.5
∠ABN=67.5![]() ,∠BAC=
,∠BAC=![]() ∠BAO=22.5
∠BAO=22.5![]() ,
,
![]() ∠C=∠ABE-∠BAC=45
∠C=∠ABE-∠BAC=45![]() ,
,
(2)同理:∠ABN=∠AOB+∠BAO=90![]() +60
+60![]() =150
=150![]()
![]() BE平分∠ABN,AC平分∠BAO,
BE平分∠ABN,AC平分∠BAO,
![]() ∠ABE=
∠ABE=![]() ∠ABN=75
∠ABN=75![]() ,∠BAC=
,∠BAC=![]() ∠BAO=30
∠BAO=30![]() ,
,
![]() ∠C=∠ABE-∠BAC=45
∠C=∠ABE-∠BAC=45![]() ,
,
(3)∠C不随点A,B的移动而发生变化.
理由:因为∠ABN是△ABO的外角,
所以∠ABN=∠AOB+∠BAO.
因为BE平分∠ABN,AC平分∠BAO,
所以∠ABE=![]() ∠ABN,∠BAC=
∠ABN,∠BAC=![]() ∠BAO,
∠BAO,
所以∠C=∠ABE-∠BAC=![]() (∠AOB+∠BAO)-
(∠AOB+∠BAO)-![]() ∠BAO=
∠BAO=![]() ∠AOB.
∠AOB.
因为∠AOB=∠MON=90°,
所以∠C=45°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目