题目内容
【题目】（1）叙述并证明三角形内角和定理（证明用图 1）；
（2）如图 2 是七角星形，求∠A+∠B+∠C+∠D+∠E+∠F+∠G 的度数．
【答案】(1)见解析;(2) 180°
【解析】
（1）先写出已知、求证，再画图，然后证明．过点A作MN∥BC，利用MN∥BC，可得∠B=∠MAB，∠C=∠NAC，而∠MAB+∠NAC+∠BAC=180°，利用等量代换可证∠BAC+∠B+∠C=180°；
（2）先根据△外角的性质得出∠D+∠G=∠CMD，∠A+∠E=∠DMN，∠B+∠F=∠MNC，再由三角形内角和定理即可得出结论．
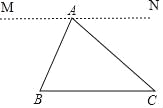
(1)证明：如图，过点 A 作直线 MN，使 MN∥BC，，
∵MN∥BC，
∴∠B=∠MAB，∠C=∠NAC（两直线平行，内错角相等）
∵∠MAB+∠NAC+∠BAC=180°（平角定义）
∴∠B+∠C+∠BAC=180°（等量代换）
∴∠BAC+∠B+∠C=180°．
（2）解：如图 2，
∵∠A+∠E=∠DME，∠G+∠D=∠ANG，∠C+∠F=∠BHC，
∵∠DME+∠ANG=∠BPH，
∴∠A+∠E+∠G+∠D=∠BPH，
∵∠B+∠BHC+∠BPH=180°，
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G=180°．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
