Question

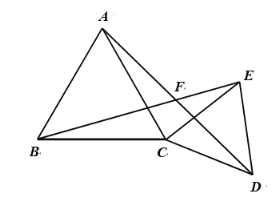
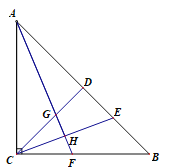
【题目】等腰Rt△ABC，点D为斜边AB上的中点，点E在线段BD上，连结CD，CE，作AH⊥CE，垂足为H，交CD于点G，AH的延长线交BC于点F.

（1）求证：△ADG≌△CDE.

（2）若点H恰好为CE的中点，求证：∠CGF=∠CFG.

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】

（1）根据已知条件可得出AD=CD=BD，∠CGH+∠GCH=∠AGD+∠GAD=90°，继而得出∠GAD=∠GCH，从而结论得以证明．

（2）由已知条件可得，∠CAH=∠EAH，继而得出∠AGD=∠=CGH=∠CFG．

解：（1）在等腰Rt△ABC中，

∵ 点D为斜边AB上的中点

∴ CD=AB，CD⊥AB

∵AD=AB

∴AD=CD

∵ CD⊥AB

∴ ∠ADG=∠CDE=90°

∵AH⊥CE

∴∠CGH+∠GCH=90°

∵∠AGD+∠GAD=90°

又∵∠AGD=∠CGH

∴∠GAD=∠GCH

在△△ADG和△CDE中

∵∠ADG=∠CDE=90°,AD=CD,∠GAD=∠GCH

∴△ADG≌△CDE…

（2）∵AH⊥CE，点H为CE的中点

∴AC=AE

∴∠CAH=∠EAH

∵∠CAH+∠AFC=90°

∠EAH+∠AGD=90°

∴∠AFC=∠AGD

∵∠AGD=∠CGH

∴∠AFC=∠CGH

即∠CGF=∠CFG．