题目内容
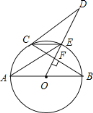
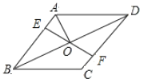
【题目】如图,O是正△ABC内一点,OA=6,OB=8,OC=10,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO',下列结论:①△BO'A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为6;③∠AOB=150°;④S△BOC=12+6![]() ; ⑤S四边形AOBO′=24+12
; ⑤S四边形AOBO′=24+12![]() .其中正确的结论是_____.(填序号)
.其中正确的结论是_____.(填序号)

【答案】①③
【解析】
证明△BO′A≌△BOC即可说明△BO'A可以由△BOC绕点B逆时针旋转60°得到,①正确;根据旋转的性质可知△BOO′是等边三角形,则点O与O'的距离为8,②错误;根据勾股定理的逆定理得到△AOO′是直角三角形,求得Rt△AOO′面积为![]() ×6×8=24,又等边△BOO′面积为
×6×8=24,又等边△BOO′面积为![]() ×8×4
×8×4![]() =16
=16![]() ,得到四边形AOBO'的面积为24+16
,得到四边形AOBO'的面积为24+16![]() ,⑤错误;求得∠AOB=∠AOO′+∠BOO′=90°+60°=150°,③正确;过B作BE⊥AO交AO的延长线于E,根据三角形的面积公式即可得到S△BOC=S四边形AOBO′﹣S△AOB=24+16
,⑤错误;求得∠AOB=∠AOO′+∠BOO′=90°+60°=150°,③正确;过B作BE⊥AO交AO的延长线于E,根据三角形的面积公式即可得到S△BOC=S四边形AOBO′﹣S△AOB=24+16![]() ﹣12=12+16
﹣12=12+16![]() ,故④错误.
,故④错误.
在△BO′A和△BOC中,
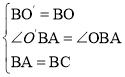 ,
,
∴△BO′A≌△BOC(SAS).
∴O′A=OC,
∴△BO'A可以由△BOC绕点B逆时针旋转60°得到,①正确;
如图1,连接OO′,根据旋转的性质可知△BOO′是等边三角形,
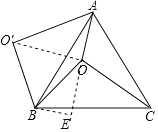
∴点O与O'的距离为8,②错误;
在△AOO′中,AO=6,OO′=8,AO′=10,
∴△AOO′是直角三角形,∠AOO′=90°.
∴Rt△AOO′面积为![]() ×6×8=24,
×6×8=24,
又等边△BOO′面积为![]() ×8×4
×8×4![]() =16
=16![]() ,
,
∴四边形AOBO'的面积为24+16![]() ,⑤错误;
,⑤错误;
∠AOB=∠AOO′+∠BOO′=90°+60°=150°,③正确;
过B作BE⊥AO交AO的延长线于E,
∵∠AOB=150°,
∴∠BOE=30°,
∵OB=8,
∴BE=4,
∴S△AOB=![]() ×4×6=12,
×4×6=12,
∴S△BOC=S四边形AOBO′﹣S△AOB=24+16![]() ﹣12=12+16
﹣12=12+16![]() ,故④错误,
,故④错误,
故答案为:①③.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案