Question

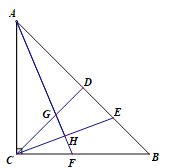
【题目】如图，OC是∠AOB的平分线，点P在OC上且OP=4，∠AOB=60°，过点P的动直线DE交OA于D，交OB于E，那么=_____．

Answer 1

【答案】 ．

【解析】

过点P作PM⊥OD于M，PN⊥OE于N，作EH⊥OD于H，再用OE表示出EH，求出S△DOE，根据角平分线的性质分别求出PM，PN，求出S△DOE，列式计算即可．

解：过点P作PM⊥OD于M，PN⊥OE于N，作EH⊥OD于H，

在Rt△EOH中，∠AOB=60°，

∴EH= OE，

∴S△DOE=×OD×EH=×OD×OE，
∵OC是∠AOB的平分线，OP=4，
∴∠MOP=∠NOP=30°，PM=PN=OP=2，
∴S△DOE=S△DOP+S△POE=×ODPM+×OEPN=OD+OE，
∴×OD×OE=OD+OE，

∴ .

故答案为：