题目内容
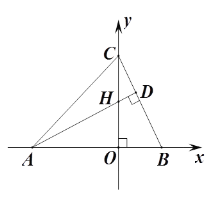
【题目】如图，在平面直角坐标系中AD⊥BC,垂足为D,交y轴于点H，直线BC的解析式为y=-2x+4.点H(0，2)，
（1）求证：△AOH≌△COB；
（2）求D点的坐标.
【答案】（1）详见解析；（2）F（
，
）
【解析】
(1)由题意可得OB=OH,∠COB=∠AOH,利用对顶角的余角可得∠HAO=∠BCO,即可证△AOH≌△COB.
(2)利用(1)中得到的条件将直线AD解析式表示出来,联立直线BC解出D即可.
证明：（1）由y=-2x+4可求得OC=4，OB=OH=2，
∵∠AOH=∠COB=90°，
∴∠HAO+∠ABC=90°
∠BCO+∠ABC=90°
即 ∠HAO=∠BCO，
∴ △AOH≌△COB（AAS）
（2）由（1）得OA=4，即A（-4,0）
∵H(0，2)，
∴于是求得直线AH解析式为：
，
联立直线BC的解析式为y=-2x+4.可求得x=，y=
∴F（，）
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
