题目内容
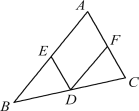
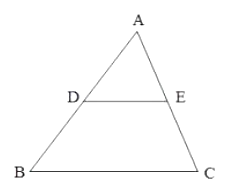
【题目】![]() 如图,在已知
如图,在已知![]() 中,
中,![]() 分别是
分别是![]() 的中点,求证
的中点,求证![]() .
.
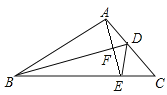
![]() 利用第
利用第![]() 题的结论,解决下列问题:
题的结论,解决下列问题:
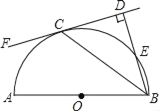
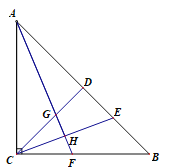
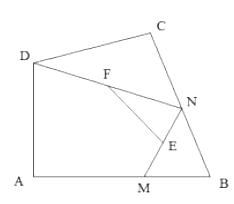
如图,在四边形![]() 中,
中,![]() ,点
,点![]() 分别在
分别在![]() 上,点
上,点![]() 分别为
分别为![]() 的中点,连接
的中点,连接![]() ,求
,求![]() 长度的最大值.
长度的最大值.
【答案】(1)证明见解析;(2)3.
【解析】
(1)延长DE到F,使得DE=EF,再证明△ADE≌△CFE,得出AD=CF和AB∥CF,则四边形DBCF为平行四边形,从而证明![]() .
.
(2)连接DM,当DM最大时,EF就最大,M与B重合DM最大,算出即可.
(1)延长DE到F,使得EF=DE,连接CF.
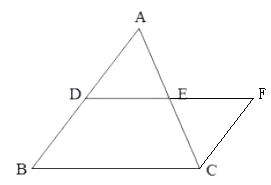
∵D、E是AB、AC的中点,
∴AD=BD,AE=CE.
∵∠AED=∠CEF,EF=DE,
∴△ADE≌△CFE(SAS)
∴CF=AD,∠DAE=∠FCE
∴BD=CD,AB∥CF,
∴四边形DBCF为平行四边形,
∴DF=BC,
∵![]()
∴![]() .
.
(2)
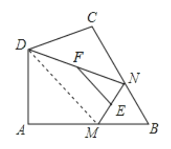
连接DM,
∵点E,F分别为MN,DN的中点,
∴EF=![]() DM,
DM,
∴DM最大时,EF最大,
∵M与B重合时DM最大,
此时DM=DB=![]() ,
,
∴EF的最大值为3.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目