ЬтФПФкШн
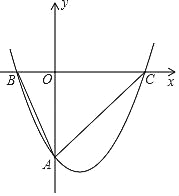
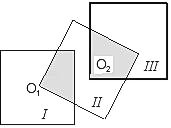
ЁОЬтФПЁПШчЭМЃЌгаШєИЩИіБпГЄЮЊ2ЕФе§ЗНаЮЃЌШєе§ЗНаЮЕФвЛИіЖЅЕуЪЧе§ЗНаЮЂёЕФжааФO1ЃЌШчЭМЫљЪОЃЌРрЫЦЕФе§ЗНаЮЂѓЕФвЛИіЖЅЕуЪЧе§ЗНаЮЂђЕФжааФO2ЃЌВЂЧве§ЗНаЮЂёгые§ЗНаЮЂѓВЛжиЕўЃЌШчЙћШєИЩИіе§ЗНаЮЖМАДетжжЗНЗЈЦДНгЃЌашвЊmИіе§ЗНаЮФмЪЙЦДНгДІЕФЭМаЮЕФвѕгАВПЗжЕФУцЛ§ЕШгквЛИіе§ЗНаЮЕФУцЛ§ЃЎЯжгавЛЮяЯпy=mx2+nx+3ЃЌЦфЖЅЕудкxжсЩЯЃЌдђИУХзЮяЯпЕФЖдГЦжсЮЊ_____ЃЎ
ЁОД№АИЁПx=ЁР![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ИљОне§ЗНаЮЕФаджЪЕУГіSЁїNO1M=![]() Sе§ЗНаЮ1ЃЌдйРћгУШЋЕШШ§НЧаЮаджЪЕУГіSЫФБпаЮNCO1E=SЁїNO1MЃЌЭЌРэПЩЕУИївѕгАУцЛ§гые§ЗНаЮЙиЯЕЃЌМДПЩЧѓГіmЕФжЕЃЌШЛКѓИљОнЖЅЕузнзјБъЕШгк0ЧѓГіnЕФжЕЃЌДгЖјПЩЧѓГіКЏЪ§ЕФЖдГЦжсЃЎ
Sе§ЗНаЮ1ЃЌдйРћгУШЋЕШШ§НЧаЮаджЪЕУГіSЫФБпаЮNCO1E=SЁїNO1MЃЌЭЌРэПЩЕУИївѕгАУцЛ§гые§ЗНаЮЙиЯЕЃЌМДПЩЧѓГіmЕФжЕЃЌШЛКѓИљОнЖЅЕузнзјБъЕШгк0ЧѓГіnЕФжЕЃЌДгЖјПЩЧѓГіКЏЪ§ЕФЖдГЦжсЃЎ
Ждгке§ЗНаЮЂёгые§ЗНаЮЂђЃЌ
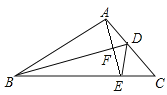
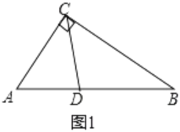
Й§O1зїе§ЗНаЮЕФБпANЁЂMNЕФДЙЯпO1FЁЂO1EЃЌДЙзуЗжБ№ЮЊFЁЂEЃЌСЌНгO1NЁЂO1MЃЎ
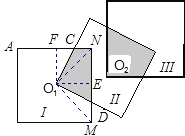
ЁпO1ЮЊе§ЗНаЮЂёЕФжааФЃЌ
ЁрO1N=O1MЃЌЁЯO1NC=ЁЯO1MD=45ЁуЃЌЁЯNO1M=90ЁуЃЌ
SЁїNO1M=![]() Sе§ЗНаЮ1ЃЌ
Sе§ЗНаЮ1ЃЌ
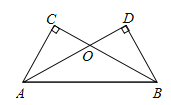
ЁпЁЯCO1N+ЁЯNO1D=ЁЯCO1D=90ЁуЃЌЁЯDO1M+ЁЯNO1D=ЁЯNO1M=90ЁуЃЌ
ЁрЁЯCO1N=ЁЯDO1MЃЎ
дкЁїNCO1гыЁїMDO1жаЃЌ
ЁпЁЯO1NC=ЁЯO1MDЃЌO1N=O1MЃЌЁЯCO1N=ЁЯDO1MЃЌ
ЁрЁїNCO1ЁеЁїMDO1ЃЈASAЃЉЃЌ
ЁрSЁїNCO1=SЁїMDO1ЃЌ
ЁрSЫФБпаЮNCO1D=SЁїNO1MЃЌ
МДе§ЗНаЮЂёгые§ЗНаЮЂђжиКЯВПЗжЕФвѕгАВПЗжУцЛ§ЮЊе§ЗНаЮУцЛ§ЕФ![]() ЃЌ
ЃЌ
ЁрашвЊ5ИіаЁе§ЗНаЮФмЪЙЦДНгГіЕФЭМаЮЕФвѕгАВПЗжУцЛ§ЕШгквЛИіаЁе§ЗНаЮЕФУцЛ§ЃЎ
Ёрm=5ЃЌ
ЁпЮяЯпy=5x2+nx+3ЕФЖЅЕудкxжсЩЯЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёрn=ЁР2![]() ,
,
Ёрy=5x2ЁР2![]() x+3
x+3
ЁрЖдГЦжсx=ЁР![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЃКx=ЁР![]() ЃЎ
ЃЎ