Question

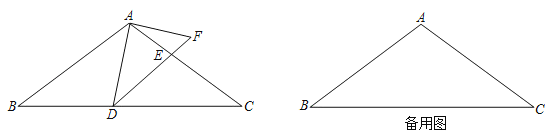
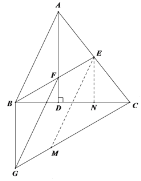
【题目】如图，△ABC的高AD与中线BE相交于点F，过点C作BE的平行线、过点F作AB的平行线，两平行线相交于点G，连接BG．

（1）若AE=2.5，CD=3，BD=2，求AB的长；

（2）若∠CBE=30°，求证：CG=AD+EF．

Answer 1

【答案】（1）；（2）见解析．

【解析】

（1）BE是△ABC的中线，则AC=5，由勾股定理求出AD的长，再由勾股定理求得AB的长；
（2）过点E作EM∥FG，作EN∥AD，先得出EN=AD，然后证明EN=BE，从而有AD=BE．再证明△ABE≌△EMC，得出BE=MC，再推导出四边形EFGM是平行四边形，得出EF=GM，继而可得出结论．

（1）解：∵BE是△ABC的中线，
∴AE=EC=2.5，∴AC=5，
∵AD是△ABC的高，
∴AD⊥BC，

，

；

（2）证明：如图，过点E作EM∥FG，作EN∥AD．

∵BE是中线，即E为AC的中点，∴EN为△ACD的中位线，∴EN=AD．

∵AD是高，∴EN⊥BC，∴∠ENB=90°．

∵∠CBE=30°，∴EN=BE．

∴AD=BE．

∵FG∥AB，EM∥FG，∴EM∥AB，

∴∠BAE=∠MEC．

∵EB∥CG，∴∠AEB=∠ECM．

在△ABE和△EMC中，

∵，

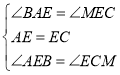∴△ABE≌△EMC（ASA），

∴BE=MC．

∵EM∥FG，BE∥GC，

∴四边形EFGM是平行四边形，

∴EF=GM．

∴GC=GM+MC=EF+BE=EF+AD．