题目内容
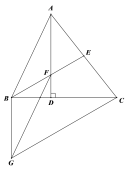
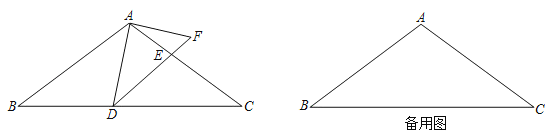
【题目】如图,在△ABC中,AB=AC=10,BC=16,点D为BC边上的一个动点(点D不与点B、点C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F.
(1)求证:ABCE=BDCD;
(2)当DF平分∠ADC时,求AE的长;
(3)当△AEF是等腰三角形时,求BD的长.
【答案】(1)见解析;(2)AE=![]() ;(3)BD的长为11或
;(3)BD的长为11或![]() 或
或![]() .
.
【解析】
(1)根据等腰三角形的性质得到∠B=∠C,根据三角形的外角性质得到∠BAD=∠CDE,得到△BAD∽△CDE,根据相似三角形的性质证明结论;
(2)证明![]() ,根据平行线的性质得到
,根据平行线的性质得到![]() =
=![]() ,证明△BDA∽△BAC,根据相似三角形的性质列式计算,得到答案;
,证明△BDA∽△BAC,根据相似三角形的性质列式计算,得到答案;
(3)分点F在DE的延长线上、点F在线段DE上两种情况,根据等腰三角形的性质计算即可.
(1)证明:∵AB=AC,
∴∠B=∠C,
∠ADC=∠BAD+∠B,∠ADE=∠B,
∴∠BAD=∠CDE,又∠B=∠C,
∴△BAD∽△CDE,
∴![]() =
=![]() ,即ABCE=BDCD;
,即ABCE=BDCD;
(2)解:∵DF平分∠ADC,
∴∠ADE=∠CDE,
∵∠CDE=∠BAD,
∴∠ADE=∠BAD,
∴![]() ,
,
∴![]() =
=![]() ,
,
∵∠BAD=∠ADE=∠B,
∴∠BAD=∠C,又∠B=∠B,
∴△BDA∽△BAC,
∴![]() =
=![]() ,即
,即![]() =
=![]()
解得,BD=![]() ,
,
∴![]() =
=![]() ,
,
解得,AE=![]() ;
;
(3)解:作AH⊥BC于H,
∵AB=AC,AH⊥BC,
∴BH=HC=![]() BC=8,
BC=8,
由勾股定理得,AH=![]() =
=![]() =6,
=6,
∴tanB=![]() =
=![]() ,
,
∴tan∠ADF=![]() =
=![]() ,
,
设AF=3x,则AD=4x,
由勾股定理得,DF=![]() =5x,
=5x,
∵△BAD∽△CDE,
∴![]() =
=![]() ,
,
当点F在DE的延长线上,FA=FE时,DE=5x﹣3x=2x,
∴![]() =
=![]() ,
,
解得,CD=5,
∴BD=BC﹣CD=11,
当EA=EF时,DE=EF=2.5x,
∴![]() =
=![]() ,
,
解得,CD=![]() ,
,
∴BD=BC﹣CD=![]() ;
;
当AE=AF=3x时,DE=![]() x,
x,
∴![]() =
=![]() ,
,
解得,CD=![]() ,
,
∴BD=BC﹣CD=![]() ;
;
当点F在线段DE上时,∠AFE为钝角,
∴只有FA=FE=3x,则DE=8x,
∴![]() =
=![]() ,
,
解得,CD=20>16,不合题意,
∴△AEF是等腰三角形时,BD的长为11或![]() 或
或![]() .
.


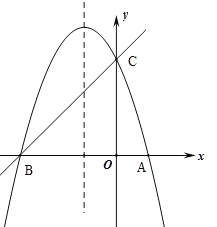
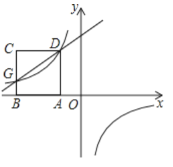
【题目】小明为探究函数![]() 的图象和性质,需要画出函数图象,列表如下:
的图象和性质,需要画出函数图象,列表如下:
| …… |
|
|
|
|
|
|
|
|
|
| …… |
| …… |
|
|
|
|
|
|
|
|
|
| …… |
根据上表数据,在平面直角坐标系中描点,画出函数图象,如图如示,小明画出了图象的一部分.
(1)请你帮小明画出完整的![]() 的图象;
的图象;
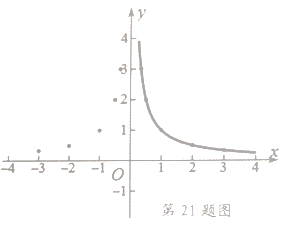
(2)观察函数图象,请写出这个函数的两条性质:
性质一: ;
性质二: .
(3)利用上述图象,探究函数![]() 图象与直线
图象与直线![]() 的关系;
的关系;
①当![]() 时, 直线
时, 直线![]() 与函数
与函数![]() 在第一象限的图象有一个交点
在第一象限的图象有一个交点![]() ,则
,则![]() 的坐标是 ;
的坐标是 ;
②当![]() 为何值时,讨论函数
为何值时,讨论函数![]() 的图象与直线
的图象与直线![]() 的交点个数.
的交点个数.