题目内容
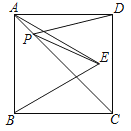
【题目】如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形内,在对角线AC上找到一点P,使PD+PE的和最小,则这个和的最小值是( )
A.![]() B.
B.![]() C.3D.
C.3D.![]()
【答案】A
【解析】
由于点B与D关于AC对称,BE与AC的交点即为P点.此时PD+PE=BE最小,而BE是等边△ABE的边,BE=AB,由正方形ABCD的面积为12,可求出AB的长,从而得出结果.
解:设BE与AC交于点P′,
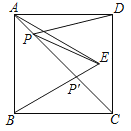
∵四边形ABCD是正方形,
∴点B与D关于AC对称,
∴P′D=P′B,
∴P′D+P′E=P′B+P′E=BE最小.
即P在AC与BE的交点上时,PD+PE最小,为BE的长度;
∵正方形ABCD的面积为12,
∴AB=![]() .
.
又∵△ABE是等边三角形,
∴BE=AB=![]() .
.
故所求最小值为![]() .
.
故选:A.

【题目】新冠肺炎疫情发生后,口罩市场出现热销,小明的爸爸用12000元购进医用外科、N95两种型号的口罩在自家药房销售,销售完后共获利2700元,进价和售价如下表:
品名价格 | 医用外科口罩 | N95口罩 |
进价(元/袋) | 20 | 30 |
售价(元/袋) | 25 | 36 |
(1)小明爸爸的药房购进医用外科、N95两种型号口罩各多少袋?
(2)该药房第二次以原价购进医用外科、N95两种型号口罩,购进医用外科口罩袋数不变,而购进N95口罩袋数是第一次的2倍,医用外科口罩按原售价出售,而效果更好的N95口罩打折让利销售,若两种型号的口罩全部售完,要使第二次销售活动获利不少于2460元,每袋N95口罩最多打几折?
【题目】丁老师为了解所任教的两个班的学生数学学习情况,对数学进行了一次测试,获得了两个班的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
①A、B两班学生(两个班的人数相同)数学成绩不完整的频数分布直方图如下(数据分成5组:x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):
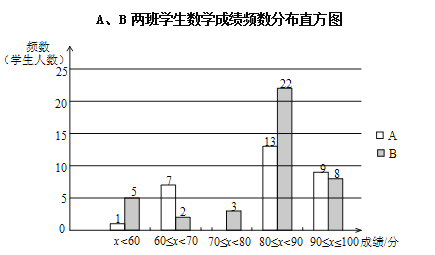
②A、B两班学生测试成绩在80≤x<90这一组的数据如下:
A班:80 80 82 83 85 85 86 87 87 87 88 89 89
B班:80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89
③A、B两班学生测试成绩的平均数、中位数、方差如下:
平均数 | 中位数 | 方差 | |
A班 | 80.6 | m | 96.9 |
B班 | 80.8 | n | 153.3 |
根据以上信息,回答下列问题:
(1)补全数学成绩频数分布直方图;
(2)写出表中m、n的值;
(3)请你对比分析A、B两班学生的数学学习情况(至少从两个不同的角度分析).