题目内容
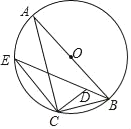
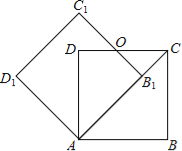
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
连接AC1,AO,根据四边形AB1C1D1是正方形,得出∠C1AB1=∠AC1B1=45°,求出∠DAB1=45°,推出A、D、C1三点共线,在Rt△C1D1A中,由勾股定理求出AC1,进而求出DC1=OD,根据三角形的面积计算即可.
连接AC1,
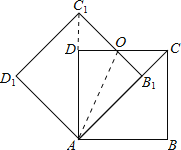
∵四边形AB1C1D1是正方形,
∴∠C1AB1=![]() ×90°=45°=∠AC1B1,
×90°=45°=∠AC1B1,
∵边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,
∴∠B1AB=45°,
∴∠DAB1=90°-45°=45°,
∴AC1过D点,即A、D、C1三点共线,
∵正方形ABCD的边长是1,
∴四边形AB1C1D1的边长是1,
在Rt△C1D1A中,由勾股定理得:AC1=![]() ,
,
则DC1=![]() -1,
-1,
∵∠AC1B1=45°,∠C1DO=90°,
∴∠C1OD=45°=∠DC1O,
∴DC1=OD=![]() -1,
-1,
∴S△ADO=![]() ×ODAD=
×ODAD=![]() ,
,
∴四边形AB1OD的面积是=2×![]() =
=![]() -1,
-1,
故选C.

【题目】今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.
对雾霾了解程度的统计表:
对雾霾的了解程度 | 百分比 |
A.非常了解 | 5% |
B.比较了解 | m |
C.基本了解 | 45% |
D.不了解 | n |
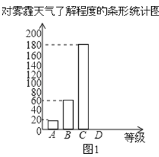
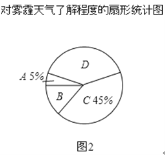
请结合统计图表,回答下列问题.
(1)本次参与调查的学生共有 人,m= ,n= ;
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是 度;
(3)请补全条形统计图;
(4)根据调查结果,学校准备开展关于雾霾知识竞赛,某班要从“非常了解”态度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.