题目内容
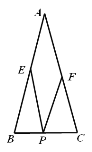
【题目】已知:如图![]() ,在
,在![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 的中点.以
的中点.以![]() 为直径作圆
为直径作圆![]() ,交边
,交边![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() .
.
![]() 求证:
求证:![]() 是圆
是圆![]() 的切线;
的切线;
![]() 当
当![]() 时,求证:
时,求证:![]() ;
;
![]() 如图
如图![]() ,当
,当![]() 是圆
是圆![]() 的切线,
的切线,![]() 为
为![]() 中点,
中点,![]() ,求
,求![]() 的长.
的长.

【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据等腰三角形的三线合一的性质可得AD⊥BD,即可判定![]() 是圆
是圆![]() 的切线;(2)连接PD,根据直径所对的圆周角是直角可得∠BPD=90°,即可得PD∥AC;已知点D是边BC的中点,可得
的切线;(2)连接PD,根据直径所对的圆周角是直角可得∠BPD=90°,即可得PD∥AC;已知点D是边BC的中点,可得![]() =
=![]() BC;再由
BC;再由![]() ,可判定△BPD∽△BAC、△PED∽△CEA,根据相似三角形的性质可得
,可判定△BPD∽△BAC、△PED∽△CEA,根据相似三角形的性质可得![]() ,
,![]() ,即可证得
,即可证得![]() ;(3)(3)连接OP,可求得
;(3)(3)连接OP,可求得![]() ,
,![]() ,
,![]() ;根据切线的性质可得
;根据切线的性质可得![]() .根据由勾股定理求得
.根据由勾股定理求得![]() ;在
;在![]() 中可
中可![]() ,在Rt
,在Rt![]() 中,
中,![]() ,由此求得
,由此求得![]() .即可求得
.即可求得![]() .
.
根据三角函数可求得PC,CD的长,再在RT△ADE中利用三角函数求得DE的长,进而得出AD的长.
![]() 证明:∵
证明:∵![]() ,点
,点![]() 是边
是边![]() 的中点,
的中点,
∴![]() .
.
又∵![]() 是圆
是圆![]() 直径,
直径,
∴![]() 是圆
是圆![]() 的切线.
的切线.
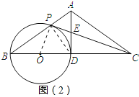
![]() 证明:连接
证明:连接![]() ,则∠BPD=90°,
,则∠BPD=90°,
∵![]() ,
,
∴![]() ,
,
∵点D是边BC的中点,
∴![]() =
=![]() BC,
BC,
∵![]() ,
,
∴△BPD∽△BAC,△PED∽△CEA,
∴![]() ,
,![]()
∴![]() ;
;
![]() 连接
连接![]() ,
,
由![]() ,得
,得![]() ,
,![]() ,
,![]() ,
,
∵![]() 是圆
是圆![]() 的切线,
的切线,![]() 为圆心,
为圆心,
∴![]() .∴由勾股定理,得
.∴由勾股定理,得![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,![]() .
.
∵![]() 为
为![]() 中点,
中点,
∴![]() .
.

练习册系列答案
相关题目