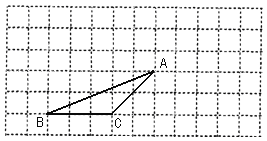
题目内容
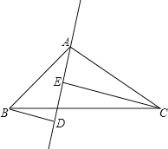
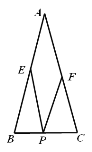
【题目】如图,在△ABC中,AB=AC=4,BC=2,点P、E、F分别为边BC、AB、AC上的任意点,则PE+PF的最小值是_____.
【答案】![]()
【解析】
当PE⊥AB,PF⊥AC时,PE+PF的值最小.
解:如图,作CG⊥AB于G,PH⊥CG于H,
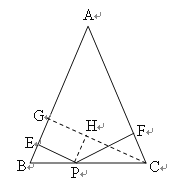
当PE⊥AB,PF⊥AC时,则∠EGH=GHP=∠PEG=90°,
∴四边形PEGH为矩形,
∴PE=HG,PH∥AB,
∴∠B=∠HPC,
∵AB=AC,
∴∠B=∠FCP,
∴∠HPC=∠FCP,
∵∠PHC=∠CFP=90°,PC=CP,
∴△PHC≌△CFP(AAS),
∴CH=PF
∴PE+PF=HG+CH=CG,
故此时PE+PF将取得最小值.
在Rt△ACG中,
∵AC=4,
∴CG2=AC2-AG2=42-AG2,
在Rt△BCG中,
∵BC=2,BG=AB-AG=4-AG,
∴CG2=BC2-BG2=22-(4-AG)2,
∴42-AG2=22-(4-AG)2,
∴AG=![]() ,
,
∴CG=![]() =
=![]() =
=![]() ,
,
∴PE+PF=![]() ,
,
即PE+PF的最小值为![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目