题目内容
【题目】矩形纸片ABCD中，已知AD=8，AB=6，E是边BC上的点，以AE为折痕折叠纸片，使点B落在点F处，连接FC，当△EFC为直角三角形时，BE的长为 ．
【答案】3或6
【解析】试题分析：
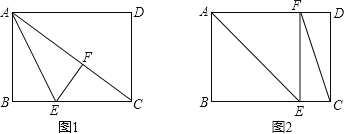
由题意可知有两种情况，见图1与图2；
图1：当点F在对角线AC上时，∠EFC=90°，
∵∠AFE=∠B=90°，∠EFC=90°，
∴点A、F、C共线，
∵矩形ABCD的边AD=8，
∴BC=AD=8，
在Rt△ABC中，AC=
=10，
设BE=x，则CE=BC﹣BE=8﹣x，
由翻折的性质得，AF=AB=6，EF=BE=x，
∴CF=AC﹣AF=10﹣6=4，
在Rt△CEF中，EF2+CF2=CE2，
即x2+42=（8﹣x）2，
解得x=3，
即BE=3；
图2：当点F落在AD边上时，∠CEF=90°，
由翻折的性质得，∠AEB=∠AEF=
×90°=45°，
∴四边形ABEF是正方形，
∴BE=AB=6，
综上所述，BE的长为3或6．
故答案为：3或6．
【题目】小明和小颖做掷骰子的游戏，规则如下：
① 游戏前，每人选一个数字；
② 每次同时掷两枚均匀骰子；
③ 如果同时掷得的两枚骰子点数之和，与谁所选数字相同，那么谁就获胜．
（1）在下表中列出同时掷两枚均匀骰子所有可能出现的结果：
第2枚骰子掷得 第1枚 的点数 骰子掷得的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
1 | ||||||
2 | ||||||
3 | ||||||
4 | ||||||
5 | ||||||
6 |
（2）小明选的数字是5，小颖选的数字是6．如果你也加入游戏，你会选什么数字，使自
己获胜的概率比他们大？请说明理由.
【题目】上周“双十二”瑞安某书店开展优惠购书活动：各类课外书活动时每本销售价格为y元，活动前每本销售价格为x（
）元，且y是x的一次函数，其中A类课外书与B类课外书活动前与活动时的价格如下表：
图书类别 | 活动前的每本销售价格x（单位：元） | 活动时的每本销售价格y （单位：元） |
A类 | 28 | 21 |
B类 | 21 | 18 |
（1）求y关于x的一次函数表达式.
（2）当天小明购买了一本课外书，花费了24元，该课外书活动前的每本销售价格是多少元？
（3）在“双十二”优惠活动中，某学校花费不超过1900元，购买A、B两类课外书共100本，且B类课外书不超过70本，则可能有哪几种购书方案？