题目内容
【题目】（1）已知y=（m2+m）
+（m﹣3）x+m2是x的二次函数，求出它的解析式．
（2）用配方法求二次函数y=﹣x2+5x﹣7的顶点坐标并求出函数的最大值或最小值．
【答案】（1）由题意可得：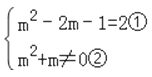
，
解①得：m1=3，m2=﹣1，
由②得：m≠0且m≠﹣1，
∴m=3，
∴y=12x2+9；
（2）y=﹣x2+5x﹣7
=﹣（x2﹣5x+
﹣）﹣7
=﹣（x﹣
）2+﹣7
=﹣（x﹣）2﹣
． ，
顶点坐标为：（， ﹣），有最大值为：﹣．
【解析】试题分析：（1）直接利用二次函数的定义得出等式求出即可；
（2）利用配方法求出其顶点坐标即可．
试题解析：(1)由题意可得： 
解①得： 
由②得：m≠0且m≠1，
∴m=3，
(2) 
顶点坐标为： 
有最大值为： 
练习册系列答案
相关题目
