题目内容
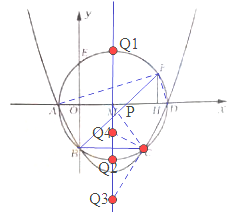
【题目】(本题满分12分)如图,在平面直角坐标系中,抛物线![]() 与⊙M相交于A、B、C、D四点.其中AB两点的坐标分别为(-1,0),(0,-2),点D在
与⊙M相交于A、B、C、D四点.其中AB两点的坐标分别为(-1,0),(0,-2),点D在![]() 轴上且AD为⊙M的直径.点E是⊙M与
轴上且AD为⊙M的直径.点E是⊙M与![]() 轴的另一个交点,过劣弧
轴的另一个交点,过劣弧![]() 上的点F作FH⊥AD于点H,且FH=1.5.
上的点F作FH⊥AD于点H,且FH=1.5.

(1)求点D的坐标及该抛物线的表达式;
(2)若点P是![]() 轴上的一个动点,试求出⊿PEF的周长最小时点P的坐标;
轴上的一个动点,试求出⊿PEF的周长最小时点P的坐标;
(3)在抛物线的对称轴上是否存在点Q,使⊿QCM是等腰三角形?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
【答案】(1)(4,0),![]() ;(2)P(2,0);
;(2)P(2,0);
(3)Q![]() (
(![]() ,
,![]() ),Q
),Q![]() (
(![]() ,-
,-![]() ),Q
),Q![]() (
(![]() ,-4),∴Q
,-4),∴Q![]() (
(![]() ,-
,-![]() ).
).
【解析】
试题分析:(1)根据题意,设点M的坐标为(![]() ,0),根据两点间的距离公式(半径相等)可以求得
,0),根据两点间的距离公式(半径相等)可以求得![]() ,则点D的坐标为(4,0),这样就可以根据交点式来求解抛物线的解析式:
,则点D的坐标为(4,0),这样就可以根据交点式来求解抛物线的解析式:![]() =
=![]() ;
;
(2)要在![]() 轴上的找到一点P,使得⊿PEF的周长最小,我们先来看E,F两点,这是两个定点,也就是说EF的长度是不变的,那实际上这个题目就是求PE+PF的最小值,这就变成了轴对称问题中最为经典的“放羊问题”,要解决这一问题首先我们看图中有没有E或F的对称点,根据题意,显然是有E点的对称点B的,那么连接BF与
轴上的找到一点P,使得⊿PEF的周长最小,我们先来看E,F两点,这是两个定点,也就是说EF的长度是不变的,那实际上这个题目就是求PE+PF的最小值,这就变成了轴对称问题中最为经典的“放羊问题”,要解决这一问题首先我们看图中有没有E或F的对称点,根据题意,显然是有E点的对称点B的,那么连接BF与![]() 轴的交点就是我们要求的点P(2,0);
轴的交点就是我们要求的点P(2,0);
(3)首先点M本身就在抛物线对称轴上,其坐标为![]() ;点C是点B关于抛物线对称轴的对称点,所以点C的坐标为(3,-2);求Q点的坐标,根据题意可设Q点为(
;点C是点B关于抛物线对称轴的对称点,所以点C的坐标为(3,-2);求Q点的坐标,根据题意可设Q点为(![]() ).⊿QCM是等腰三角形,则可能有三种情况,分别是QC=MC;QM=MC;QC=QM.根据这三种情况就能求得Q点的坐标可能是
).⊿QCM是等腰三角形,则可能有三种情况,分别是QC=MC;QM=MC;QC=QM.根据这三种情况就能求得Q点的坐标可能是![]() 或
或![]() 或
或![]() .
.
试题解析:(1)∵A(-1,0),B(0,-2)
∴OE=OB=2,OA=1,
∵AD是⊙M的直径,
∴OE·OB=OA·OD,
即:2=1·OD,OD=4,
∴D(4,0),
把A(-1,0),B(0,-2),D(4,0)代入![]() 得:
得:
 ,即
,即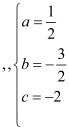
该抛物线的表达式为:![]() .
.
连接AF,DF,
∵FH⊥AD于点H,AD为直径
∴△AFH∽△FDH,
∴HF=DH·AH,
∵E点与B点关于点O对称,
根据轴对称的性质,连接BF交x轴于点P,
∵A(-1,0),D(4,0),
∴AD=5,
设DH=x,则AH=5-x,
即1.5=x(5-x),
5x-x=![]() ,
,
4x-20x+9=0,
(2x-1)(2x-9)=0,
由AH>DH,
∴DH=![]() ,
,
∴OH=OD-DH=![]() ,
,
∴F(3.5,1.5),
设直线BF的解析式为![]() ,
,
则3.5k+b=1.5;b=-2,
则k=1,b=-2,
∴y=x-2,
令y=0,则x=-2,
∴P(2,0)
(3)Q![]() (
(![]() ,
,![]() ),Q
),Q![]() (
(![]() ,-
,-![]() ),Q
),Q![]() (
(![]() ,-4
,-4![]() (
(![]() ,-
,-![]() ).
).