��Ŀ����
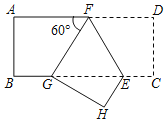
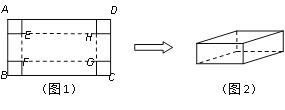
����Ŀ����һ���㹻���ֽ���Ͻ�ȡһ�����Ϊ3600ƽ�����ľ���ֽ��ABCD����ͼ1�����ھ���ֽ����ĸ�������ȥ�߳���ȵ�С�����Σ��ٰ����ı���������������һ���ǵij�����ֽ�У�����Ϊ����EFGH����ͼ2����С�����εı߳�Ϊx���ף�
��1��������ֽ��ABCD��һ�߳�Ϊ90����ʱ����ֽ�еIJ���������ֵ��
��2����EH��EF��7��2���Ҳ����������֮��Ϊ9��7ʱ����x��ֵ��
���𰸡���1��![]() ����2��10.
����2��10.
�������������������1����a=90ʱ��b=40�����������������䷽����ֽ�в���������ֵ��
��2�����������з�����⼴��.
���������
��1��S����2[x(90��2x)��x(40��2x)] ����8x2��260x
����8(x��![]() )2��
)2��![]() ��
��
����8��0���൱x��![]() ʱ��S�����
ʱ��S�����![]() ��
��
��2����EF��2m����EH��7m��
������Ϊ2(7mx��2mx)��18mx�������Ϊ7m��2m��14m��
�����⣬��18mx��14m��9��7����m��x��
��AD��7x��2x��9x��AB��2x��2x��4x
��4x��9x��3600����x��0��
��x��10��

��ϰ��ϵ�д�
 ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�
�����Ŀ